题目内容
1.若不等式组$\left\{\begin{array}{l}{x+1<a①}\\{3x+5>x-7②}\end{array}\right.$有解,求实数a的取值范围.分析 首先利用a表示出不等式组的解集,根据不等式组有解,即可确定a的取值范围.
解答 解:$\left\{\begin{array}{l}{x+1<a①}\\{3x+5>x-7②}\end{array}\right.$
解不等式①得x<a-1,
解不等式②得x>-6,
∵不等式组有解,
∴-6<x<a-1
则a-1>-6,
a>-5.
点评 此题考查不等式组的解法.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
8.平面上有n个点(n≥2)且任意三个点不在同一直线上,过这些点中的任两点作直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可作出3条直线;当有4个点时,可作出6条直线;当有5个点时,可作出10条直线,当有6点时,可作出15条直线.
②归纳:考察点的个数n和可作出直线的条数Sn发现如下表所示:Sn=$\frac{n(n-1)}{2}$.
③当有2006个点时,可作出直线的条数S2006=2011015.
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可作出3条直线;当有4个点时,可作出6条直线;当有5个点时,可作出10条直线,当有6点时,可作出15条直线.
②归纳:考察点的个数n和可作出直线的条数Sn发现如下表所示:Sn=$\frac{n(n-1)}{2}$.
| 点的个数 | 可连成直线条数 |
| 2 | l=S2=$\frac{2×1}{2}$ |
| 3 | 3=S3=$\frac{3×2}{2}$ |
| 4 | 6=S4=$\frac{4×3}{2}$ |
| 5 | 10=S5=$\frac{5×4}{2}$ |
| … | … |
| n | Sn=$\frac{n(n-1)}{2}$ |
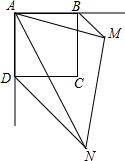 已知:如图,正方形ABCD,BM、DN分别是正方形的两个外角平分线,∠MAN=45°,将∠MAN绕着正方形的顶点A旋转,边AM、AN分别交两条角平分线于点M、N,联结MN.
已知:如图,正方形ABCD,BM、DN分别是正方形的两个外角平分线,∠MAN=45°,将∠MAN绕着正方形的顶点A旋转,边AM、AN分别交两条角平分线于点M、N,联结MN. 如图,在平行四边形ABCD中,∠FCD=∠EAB,∠BCE=∠DAF,求证:四边形FAEC是平行四边形.
如图,在平行四边形ABCD中,∠FCD=∠EAB,∠BCE=∠DAF,求证:四边形FAEC是平行四边形.