题目内容
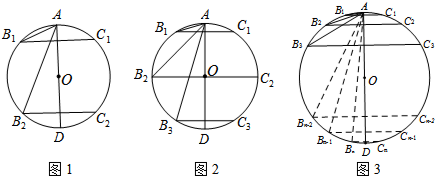
10.如图,AD是⊙O的直径.(1)如图1,垂直于AD的两条弦B1C1,B2C2把圆周4等分,则∠B1的度数是22.5°,∠B2的度数是67.5°;
(2)如图2,垂直于AD的三条弦B1C1,B2C2,B3C3把圆周6等分,则∠B3的度数是75°;
(3)如图3,垂直于AD的n条弦B1C1,B2C2,B3 C3,…,BnCn把圆周2n等分,则∠Bn的度数是90°-$\frac{45°}{n}$(用含n的代数式表示∠Bn的度数).
分析 (1)求出每条弧的度数,求出所求的圆周角所对的弧的度数,最后根据圆周角定理(圆周角的度数等于它所对的弧的度数的一半)得出即可;
(2)求出每条弧的度数,求出所求的圆周角所对的弧的度数,最后根据圆周角定理(圆周角的度数等于它所对的弧的度数的一半)得出即可;
(3)求出每条弧的度数,求出所求的圆周角所对的弧的度数,最后根据圆周角定理(圆周角的度数等于它所对的弧的度数的一半)得出即可.
解答 解:(1)∵垂直于AD的两条弦B1C1,B2C2把圆周4等分,
∴弧B1C1、弧C1C2、弧B2C2、弧B1B2的度数都是90°,弧AB1=弧AC1,
∴弧AC1的度数是45°,
∴∠B1=$\frac{1}{2}$×45°=22.5°,
∠B2=$\frac{1}{2}$×(45°+90°)=67.5°,
故答案为:22.5°,67.5°;
(2)∵垂直于AD的三条弦B1C1,B2C2,B3C3把圆周6等分
∴弧B1C1、弧C1C2、弧C2C3的度数都是60°,弧AB1=弧AC1,
∴弧AC1的度数是30°,
∴∠B3=$\frac{1}{2}$×(30°+60°+60°)=75°,
故答案为:75°;
(3)∵垂直于AD的n条弦B1C1,B2C2,B3 C3,…,BnCn把圆周2n等分,
∴弧B1C1、弧C1C2、弧C2C3、…的度数都是($\frac{360}{2n}$)°=($\frac{180}{n}$)°,弧AB1=弧AC1,
∴弧AC1的度数是($\frac{90}{n}$)°,
∴∠Bn=$\frac{1}{2}$×($\frac{90}{n}$+$\frac{180}{n}$+$\frac{180}{n}$+…+$\frac{90}{n}$)=$\frac{1}{2}$×[$\frac{(n-1)•180}{n}$+$\frac{90}{n}$]°=90°-$\frac{45°}{n}$
故答案为:90°-$\frac{45°}{n}$.
点评 本题考查了圆周角定理的应用,能正确运用定理进行计算是解此题的关键,注意:圆心角的度数等于它所对的弧的度数,圆周角等于它所夹弧所对的圆心角的一半,难度适中.

 阅读快车系列答案
阅读快车系列答案
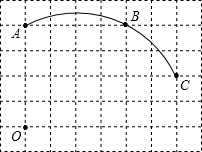 如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.
如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.
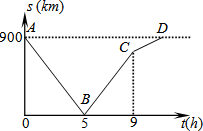 一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,沿同一条道路匀速行驶.设行驶时间为t(h),两车之间的距离为s(km),图中折线A-B-C-D表示s与t之间的函数关系.
一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,沿同一条道路匀速行驶.设行驶时间为t(h),两车之间的距离为s(km),图中折线A-B-C-D表示s与t之间的函数关系.
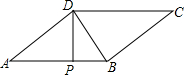 如图,?ABCD中,DP⊥AB于P,且PD2=AP•PB,△BCD的面积和周长分别为24和24,求PD的长.
如图,?ABCD中,DP⊥AB于P,且PD2=AP•PB,△BCD的面积和周长分别为24和24,求PD的长.