题目内容
20．
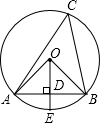如图，AB是⊙O的弦，OD⊥AB于D交⊙O于E，则下列说法错误的是（ ）| A． | ∠ACB=∠AOE | B． | AD=BD | C． | S△AOB=$\frac{1}{2}$S△ABC | D． | AE=BE |
分析 先根据圆周角定理得出∠AOB=2∠ACB，再由垂径定理可知∠AOE=∠BOE，$\widehat{AE}$=$\widehat{BE}$，故可得出结论．
解答 解：∵∠ACB与∠AOB是同弧所对的圆周角与圆心角，
∴∠AOB=2∠ACB，
∵OD⊥AB，
∴∠AOE=∠BOE，$\widehat{AE}$=$\widehat{BE}$，
∴∠ACB=∠AOE，AD=BD，AE=BE，
∴A，B，D正确，C错误．
故选C．
点评 本题考查的是垂径定理，熟知平分弦的直径平分这条弦，并且平分弦所对的两条弧是解答此题的关键．
练习册系列答案
相关题目
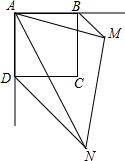已知：如图，正方形ABCD，BM、DN分别是正方形的两个外角平分线，∠MAN=45°，将∠MAN绕着正方形的顶点A旋转，边AM、AN分别交两条角平分线于点M、N，联结MN．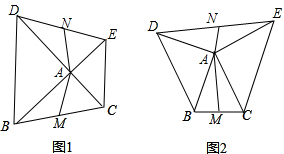
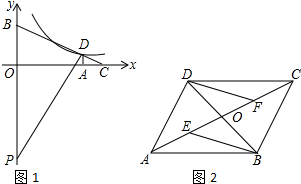
如图所示，反比例函数y1=$\frac{6}{x}$的图象与一次函数y2=kx+b的图象交于点A（3，m），B（n，-3），一次函数图象与y轴交于点C．