题目内容
3．一个角的补角的一半比这个角的余角的三分之一多40度．求这个角的度数．分析 设这个角为x，根据余角和补角的概念用x表示出这个角的余角和补角，根据题意列出方程，解方程即可．
解答 解：设这个角为x，则这个角的余角为90°-x，补角为180°-x，
由题意得$\frac{1}{3}$（90°-x）+40°=$\frac{1}{2}$（180°-x），
解得x=120°．
故这个角的度数是120°．
点评 本题考查的是余角和补角的概念，关键是熟悉如果两个角的和等于90°，这两个角互为余角；如果两个角的和等于180°，这两个角互为补角的知识点．
练习册系列答案
相关题目
11．
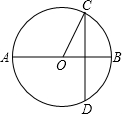如图，AB是⊙O的直径，弦CD⊥AB，∠OCD=30°，CD=2$\sqrt{3}$，则扇形BOC的面积为（ ）
如图，AB是⊙O的直径，弦CD⊥AB，∠OCD=30°，CD=2$\sqrt{3}$，则扇形BOC的面积为（ ）| A． | $\frac{2π}{3}$ | B． | $\frac{π}{3}$ | C． | π | D． | 2π |
18．
如图，梯形ABCD中，AD∥BC，DC⊥BC，将梯形沿对角线BD折叠，点A恰好落在DC边上的点A’处，若∠ABD=25°，则∠A′BC的度数为（ ）
如图，梯形ABCD中，AD∥BC，DC⊥BC，将梯形沿对角线BD折叠，点A恰好落在DC边上的点A’处，若∠ABD=25°，则∠A′BC的度数为（ ）| A． | 15° | B． | 20° | C． | 25° | D． | 30° |
15．
如图，在平面直角坐标系中，Rt△ABO中，∠ABO=90°，OB边在x轴上，将△ABO绕点B顺时针旋转60°得到△CBD．若点A的坐标为（-2，2$\sqrt{3}$），则点C的坐标为（ ）
如图，在平面直角坐标系中，Rt△ABO中，∠ABO=90°，OB边在x轴上，将△ABO绕点B顺时针旋转60°得到△CBD．若点A的坐标为（-2，2$\sqrt{3}$），则点C的坐标为（ ）| A． | （$\sqrt{3}$，1） | B． | （1，$\sqrt{3}$） | C． | （1，2） | D． | （2，1） |
12．从-2，-1，-$\frac{1}{2}$，1，2这五个数中，随机抽取一个数，记为a，若数a使关于x的不等式组$\left\{\begin{array}{l}{2x+7≥9}\\{x-a＜0}\end{array}\right.$无解，且使分式方程$\frac{a}{2x-3}$+$\frac{a-2}{2x-3}$=-1的解为正分数，那么这五个数中所有满足条件的a的值之和是（ ）
| A． | -3 | B． | -$\frac{5}{2}$ | C． | -2 | D． | -$\frac{7}{2}$ |
13．把Rt△ABC各边的长度都扩大3倍的Rt△A′B′C′，对应锐角A，A′的正弦值的关系为（ ）
| A． | sinA=3sinA′ | B． | sinA=sinA′ | C． | 3sinA=sinA′ | D． | 不能确定 |