题目内容
15. 如图,在平面直角坐标系中,Rt△ABO中,∠ABO=90°,OB边在x轴上,将△ABO绕点B顺时针旋转60°得到△CBD.若点A的坐标为(-2,2$\sqrt{3}$),则点C的坐标为( )
如图,在平面直角坐标系中,Rt△ABO中,∠ABO=90°,OB边在x轴上,将△ABO绕点B顺时针旋转60°得到△CBD.若点A的坐标为(-2,2$\sqrt{3}$),则点C的坐标为( )| A. | ($\sqrt{3}$,1) | B. | (1,$\sqrt{3}$) | C. | (1,2) | D. | (2,1) |
分析 作CH⊥x轴于H,如图,再利用旋转的性质得BC=BA=2$\sqrt{3}$,∠ABC=60°,则∠CBH=30°,然后在Rt△CBH中,利用含30度的直角三角形三边的关系可计算出CH=$\frac{1}{2}$BC=$\sqrt{3}$,BH=$\sqrt{3}$CH=3,所以OH=BH-OB=3-2=1,于是可写出C点坐标.
解答 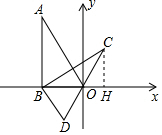 解:作CH⊥x轴于H,如图,
解:作CH⊥x轴于H,如图,
∵点A的坐标为(-2,2$\sqrt{3}$),AB⊥x轴于点B,∴tan∠BAC=$\frac{OB}{AB}$=$\frac{\sqrt{3}}{3}$,
∴∠A=30°,
∵△ABO绕点B逆时针旋转60°得到△CBD,
∴BC=BA=2$\sqrt{3}$,OB=2,∠CBH=30°,
在Rt△CBH中,CH=$\frac{1}{2}$BC=$\sqrt{3}$,
BH=$\sqrt{3}$CH=3,
OH=BH-OB=3-2=1,
∴C(1,$\sqrt{3}$).
故选:B.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.也考查了一次函数图象上点的坐标特征和含30度的直角三角形三边的关系.

练习册系列答案
相关题目
6.下列说法中正确的是( )
| A. | 两点之间的所有连线中,线段最短 | |
| B. | 射线比直线短 | |
| C. | 两条射线组成的图形叫角 | |
| D. | 小于平角的角可分为锐角和钝角两类 |
10.下列关系式中,属于二次函数的是( )
| A. | $y=\frac{1}{8}{x^2}$ | B. | y=$\sqrt{{x}^{2}-1}$ | C. | $y=\frac{1}{x^2}$ | D. | 2(x-3)2=8 |
20.在-$\sqrt{3}$,-2,0,1这四个数中,最小的数是( )
| A. | -$\sqrt{3}$ | B. | -2 | C. | 0 | D. | 1 |
7. 如图,点M,N在数轴上表示的数分别是m,n,则( )
如图,点M,N在数轴上表示的数分别是m,n,则( )
 如图,点M,N在数轴上表示的数分别是m,n,则( )
如图,点M,N在数轴上表示的数分别是m,n,则( )| A. | m+n>0 | B. | m-n>0 | C. | |m|>|n| | D. | m2<n2 |
5.下列各组整式中不是同类项的是( )
| A. | 3m2n与-4nm2 | B. | $\frac{1}{3}$xy2与$\frac{1}{3}$x2y2 | C. | -5ab与2×103ab | D. | 35与-12 |
 如图,已知抛物线y=-x2+(m-1)x+m(其中0<m<1)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l,设P为对称轴上的点,连接PA、PC
如图,已知抛物线y=-x2+(m-1)x+m(其中0<m<1)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l,设P为对称轴上的点,连接PA、PC