题目内容
19.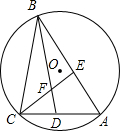 如图,△ABC内接于⊙O,∠A=60°,∠ABC、∠ACB的平分线交AC,AB于点D,E,CE,BD相交于点F,以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号是①③.
如图,△ABC内接于⊙O,∠A=60°,∠ABC、∠ACB的平分线交AC,AB于点D,E,CE,BD相交于点F,以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号是①③.
分析 ①在△ABC中,∠ABC+∠ACB=180°-∠A=120°,即∠FBC+∠FCB=60°,而∠BFE正好是△BFC的外角,即∠BFE=∠FBC+∠FCB=60°,故正确;
②若BC=BD,需满足一个条件:∠BCD=∠BDC,且看这两个角的表达式:∠BCD=180°-∠A-2∠DBA=120°-2∠DBA;∠BDC=∠BDA+∠A=60°+∠DBA;联立两式,可得∠DBA=20°;此时∠ABC=40°,而没有任何条件可以说明∠ABC的度数是40°,即可得出本选项错误.
③由于F是∠ABC和∠ACB角平分线的交点,因此F是△ABC的内心,可过F作AB、AC的垂线,通过证构建的直角三角形全等,得出FE=FD的结论,因此结论正确;
④若BF=2DF,则F是△ABC的重心,即三边中线的交点,而题目给出的条件是F是△ABC的内心,显然两者的结论相矛盾,因此不正确.
解答 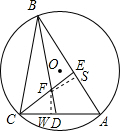 解:∵BD、CE分别是∠ABC和∠ACB的角平分线,
解:∵BD、CE分别是∠ABC和∠ACB的角平分线,
∴点F是△ABC的内心,∠CBD=$\frac{1}{2}$∠ABC,∠BCE=$\frac{1}{2}$∠ACB,
∴∠BFE=∠CBD+∠BCE
=$\frac{1}{2}$(∠CBA+∠BCA)
=$\frac{1}{2}$(180°-∠A)=60°,即cos∠BFE=$\frac{1}{2}$,故①正确;
∵∠BDC=∠A+$\frac{1}{2}$∠ABC=60°+∠DBA,∠BCA=180°-∠A-2∠DBA=120°-2∠DBA,
∴若BC=BD成立,则应有∠BDC=∠BCA,60°+∠DBA=120°-2∠DBA,即∠DBA=20°,
此时∠ABC=40°,
∴∠BCD=∠BDC=80°,
而根据题意,没有条件可以说明∠ABC是40°,
故②错误;
∵点F是△ABC内心,作FW⊥AC,FS⊥AB
则FW=FS,∠FSE=∠FWD=90°∠EFD=∠SFW=120°
∴∠SFE=∠WFD,△FSE≌△FDW,
∴FD=FE,故③正确;
由于点F是内心而不是各边中线的交点,故BF=2DF不一定成立,因此④错误.
因此本题正确的结论为①③,
故答案为:①③.
点评 本题考查了三角形的外接圆与外心、角平分线的性质、三角形内角和定理,综合性强,难度较大.要特别注意的是④中,三角形外心和重心的区别,不要混淆两者的概念.

 阅读快车系列答案
阅读快车系列答案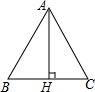 如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )
如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
①(2x+y)2=4x2+y2
②(-3b-a)(a-3b)=a2-9b2
③2×2-2=$\frac{1}{2}$
④(-1)0=-1
⑤(x-$\frac{1}{2}$)2=x2-2x+$\frac{1}{4}$
⑥(-a2)m=(-am)2.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
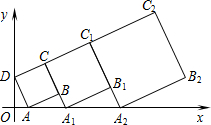 在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )| A. | 20×($\frac{3}{2}$)4030 | B. | 20×($\frac{3}{2}$)4032 | C. | 20×($\frac{3}{2}$)2016 | D. | 20×($\frac{3}{2}$)2015 |
| 队员1 | 队员2 | 队员3 | 队员4 | |
| 甲组 | 176 | 177 | 175 | 176 |
| 乙组 | 178 | 175 | 177 | 174 |
| A. | $\overline{{x}_{甲}}=\overline{{x}_{乙}}$,S甲2<S乙2 | B. | $\overline{{x}_{甲}}=\overline{{x}_{乙}}$,S甲2>S乙2 | ||
| C. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,S甲2<S乙2 | D. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,S甲2>S乙2 |
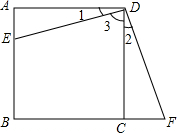 如图所示,点E是矩形ABCD的边AB上任意一点,过点D作DF⊥DE交BC的延长线于点F,DE=DF.求证:矩形ABCD是正方形.
如图所示,点E是矩形ABCD的边AB上任意一点,过点D作DF⊥DE交BC的延长线于点F,DE=DF.求证:矩形ABCD是正方形. 已知:直线y=-x-4分别交x、y轴于A、C两点,抛物线y=ax2+bx(a>0)经过A、O两点,且顶点B的纵坐标为-2
已知:直线y=-x-4分别交x、y轴于A、C两点,抛物线y=ax2+bx(a>0)经过A、O两点,且顶点B的纵坐标为-2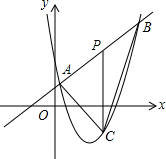 如图,直线y=x+4和抛物线y=ax2+bx+12(a≠0)相交于A(1,5)和B(8,n),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴,交抛物线于点C.
如图,直线y=x+4和抛物线y=ax2+bx+12(a≠0)相交于A(1,5)和B(8,n),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴,交抛物线于点C.