题目内容
10.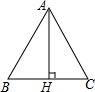 如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )
如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
分析 利用等边三角形的性质以及解直角三角形的知识求出BC的长,即可求出△ABC的面积.
解答 解:∵AB=AC=BC,
∴BH=CH=$\frac{1}{2}$CB=$\frac{1}{2}$AB,∠BAH=30°,
∵AH=$\sqrt{3}$,
∴cos30°=$\frac{AH}{AB}$,
∴AB=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2cm,
∴BC=2cm,
∴△ABC的面积为:$\frac{1}{2}$•CB•AH=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$(cm2).
故选A.
点评 本题考查了等边三角形的性质以及解直角三角形,解决问题的关键是利用解直角三角形求出BC的长.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
1.下列各图中,能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
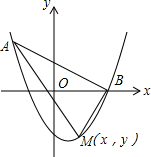 如图,点A(-2,5)在以(1,-4)为顶点的抛物线上,抛物线与x正半轴交于点B,点M(x,y)(其中-2<x<3)是抛物线上的动点,则△ABM面积的最大值为$\frac{125}{8}$.
如图,点A(-2,5)在以(1,-4)为顶点的抛物线上,抛物线与x正半轴交于点B,点M(x,y)(其中-2<x<3)是抛物线上的动点,则△ABM面积的最大值为$\frac{125}{8}$.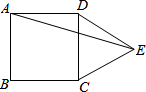 如图,在正方形ABCD的外侧,作等边三角形CDE,则∠AED的度数为15°.
如图,在正方形ABCD的外侧,作等边三角形CDE,则∠AED的度数为15°.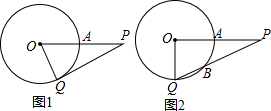 已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.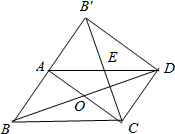 如图所示,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C,若四边形ABCD的面积为12cm2,则翻折后纸片重叠部分的面积是3cm2.
如图所示,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C,若四边形ABCD的面积为12cm2,则翻折后纸片重叠部分的面积是3cm2.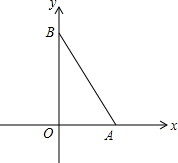 已知点A的坐标为(2,0),点B的坐标为(0,4),作等边△ABC,求点C的坐标.
已知点A的坐标为(2,0),点B的坐标为(0,4),作等边△ABC,求点C的坐标.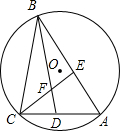 如图,△ABC内接于⊙O,∠A=60°,∠ABC、∠ACB的平分线交AC,AB于点D,E,CE,BD相交于点F,以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号是①③.
如图,△ABC内接于⊙O,∠A=60°,∠ABC、∠ACB的平分线交AC,AB于点D,E,CE,BD相交于点F,以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号是①③.