题目内容
8.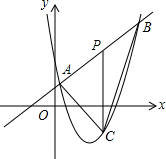 如图,直线y=x+4和抛物线y=ax2+bx+12(a≠0)相交于A(1,5)和B(8,n),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴,交抛物线于点C.
如图,直线y=x+4和抛物线y=ax2+bx+12(a≠0)相交于A(1,5)和B(8,n),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴,交抛物线于点C.(1)求抛物线的解析式;
(2)是否存在这样的点P,使△ABC的面积有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)当以线段PC为直径的圆经过点A时,求点P的坐标.
分析 (1)根据自变量与函数值的对应关系,可得B点坐标,根据待定系数法,可得函数解析式;
(2)平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,根据三角形的面积,可得二次函数,根据二次函数的性质,可得答案;
(3)根据圆的直径与半径之间的关系,可得关于m的方程,根据解方程,可得m的值,根据自变量与函数值的对应关系,可得答案.
解答 解:(1)∵点B(8,n)在直线y=x+4上,
∴n=8+4=12.
∵A(1,5),B(8,12)在抛物线y=ax2+bx+12(a≠0)上,
∴$\left\{\begin{array}{l}{5=a+b+12}\\{12=64a+8b+12}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-8}\end{array}\right.$,
故抛物线y=x2-8x+12;(
2)设动点P的坐标为(m,m+4),则点C的坐标为(m,m2-8m+12),
∴BC=(m+4)-(m2-8m+12)=-m2+9m-8;
S△ABC=$\frac{1}{2}$(8-1)(-m2+9m-8)=-$\frac{7}{2}$(m-$\frac{9}{2}$)2+$\frac{343}{8}$,
当m=$\frac{9}{2}$时,△ABC的面积最大值,最大值为$\frac{343}{8}$.
(3)∵以线段PC为直径的圆经过点A,
∴∠PAC=90°,
∴点A到PC的距离为$\frac{1}{2}$PC,
∴m-1=$\frac{1}{2}$(-m2+9m-8),
∴m=6,m=1(不符合题意,舍),
∴点P(6,10).
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用三角形的面积得出二次函数的性质是解题关键;利用圆的直径与半径之间的关系得出关于m的方程是解题关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 1.2×105 | B. | 1.2×106 | C. | 1.2×107 | D. | 1.2×108 |
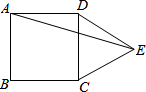 如图,在正方形ABCD的外侧,作等边三角形CDE,则∠AED的度数为15°.
如图,在正方形ABCD的外侧,作等边三角形CDE,则∠AED的度数为15°.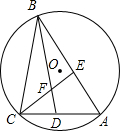 如图,△ABC内接于⊙O,∠A=60°,∠ABC、∠ACB的平分线交AC,AB于点D,E,CE,BD相交于点F,以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号是①③.
如图,△ABC内接于⊙O,∠A=60°,∠ABC、∠ACB的平分线交AC,AB于点D,E,CE,BD相交于点F,以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号是①③. 已知长度分别为3,6,2x-1的三条正整数长线段可以组成一个三角形.
已知长度分别为3,6,2x-1的三条正整数长线段可以组成一个三角形.