题目内容
7. 已知:直线y=-x-4分别交x、y轴于A、C两点,抛物线y=ax2+bx(a>0)经过A、O两点,且顶点B的纵坐标为-2
已知:直线y=-x-4分别交x、y轴于A、C两点,抛物线y=ax2+bx(a>0)经过A、O两点,且顶点B的纵坐标为-2(1)判断点B是否在直线AC上,并求该抛物线的函数关系式;
(2)以点B关于x轴的对称点D为圆心,以OD为半径作⊙D,试判断直线AC与⊙D的位置关系,并说明理由;
(3)若E为⊙D的优弧AO上一动点(不与A、O重合),连结AE、OE,问在抛物线上是否存在点P,使∠POA:∠AEO=2:3?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.
分析 (1)可先求出点A、C的坐标,然后结合点A的坐标及顶点B的纵坐标为-2可得到关于a、b的方程组,然后解这个方程组,就可得到抛物线的函数关系式,从而得到点B的坐标,然后把点B的坐标代入直线AC的解析式,就可解决问题;
(2)连接DA,如图1,要证直线AC与⊙D相切,只需证∠DAC=90°;
(3)过点P作PH⊥x轴于H,如图2①、图2②,易得∠ADO=90°,根据圆周角定理可得∠AEO,从而求出∠POA,从而可得到直线OP的解析式,然后解直线OP与抛物线的解析式组成的方程组,就可得到点P的坐标.
解答 解:(1)∵点A、C分别是直线y=-x-4与x、y轴的交点,
∴点A(-4,0),点C(0,-4),
由题意可得:$\left\{\begin{array}{l}{16a-4b=0}\\{\frac{0-{b}^{2}}{4a}=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴抛物线的函数关系式为y=$\frac{1}{2}$x2+2x.
由y=$\frac{1}{2}$x2+2x=$\frac{1}{2}$(x+2)2-2得顶点B(-2,-2).
当x=-2时,y=-x-4=-2,
∴点B在直线y=-x-4上;
(2)直线AC与⊙D相切.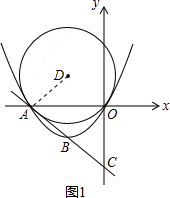 理由:连接DA,如图1.
理由:连接DA,如图1.
∵A(-4,0),C(0,-4),
∴OA=OC=4.
∵∠AOC=90°,
∴∠OAC=∠OCA=45°.
∵点B在直线AC上,
∴∠BAO=45°.
∵点B与点D关于x轴对称,
∴∠DAO=∠BAO=45°,
∴∠DAB=90°,
∵抛物线y=ax2+bx(a>0)经过A、O两点,顶点是B,点B与点D关于x轴对称,OD为半径,
∴直线AC与⊙D相切;
(3)过点P作PH⊥x轴于H,如图2①、图2②,
∵DA=DO,
∴∠DOA=∠DAO=45°,
∴∠ADO=90°.
∵E为⊙D的优弧AO上一动点(不与A、O重合),
∴∠AEO=$\frac{1}{2}$∠ADO=45°.
∵∠POA:∠AEO=2:3,
∴∠POA=$\frac{2}{3}$∠AEO=$\frac{2}{3}$×45°=30°.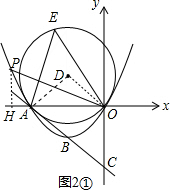 ∴直线OP的解析式为y=$\frac{\sqrt{3}}{3}$x,或y=-$\frac{\sqrt{3}}{3}$x.
∴直线OP的解析式为y=$\frac{\sqrt{3}}{3}$x,或y=-$\frac{\sqrt{3}}{3}$x.
①当直线OP的解析式为y=-$\frac{\sqrt{3}}{3}$x时,如图2①,
解方程组$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}x}\\{y=\frac{1}{2}{x}^{2}+2x}\end{array}\right.$,得
$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{2\sqrt{3}}{3}-4}\\{y=\frac{2}{3}+\frac{4\sqrt{3}}{3}}\end{array}\right.$,
∴点P的坐标为(-$\frac{2\sqrt{3}}{3}$-4,$\frac{2}{3}$+$\frac{4\sqrt{3}}{3}$).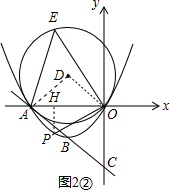 ②当直线OP的解析式为y=$\frac{\sqrt{3}}{3}$x时,如图2②,
②当直线OP的解析式为y=$\frac{\sqrt{3}}{3}$x时,如图2②,
解方程组$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x}\\{y=\frac{1}{2}{x}^{2}+2x}\end{array}\right.$,得
$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{2\sqrt{3}}{3}-4}\\{y=\frac{2}{3}-\frac{4\sqrt{3}}{3}}\end{array}\right.$,
∴点P的坐标为($\frac{2\sqrt{3}}{3}-4$,$\frac{2}{3}-\frac{4\sqrt{3}}{3}$).
综上所述:点P的坐标为(-$\frac{2\sqrt{3}}{3}$-4,$\frac{2}{3}$+$\frac{4\sqrt{3}}{3}$)或($\frac{2\sqrt{3}}{3}-4$,$\frac{2}{3}-\frac{4\sqrt{3}}{3}$).
点评 本题主要考查了运用待定系数法求抛物线解析式、等腰三角形的性质、轴对称的性质、直线与抛物线的交点等知识,运用分类讨论的思想是解决第(3)小题的关键.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案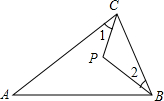 如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
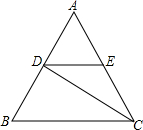 如图,△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为4,则EC的边长是2.
如图,△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为4,则EC的边长是2.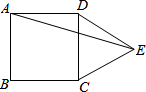 如图,在正方形ABCD的外侧,作等边三角形CDE,则∠AED的度数为15°.
如图,在正方形ABCD的外侧,作等边三角形CDE,则∠AED的度数为15°.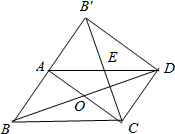 如图所示,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C,若四边形ABCD的面积为12cm2,则翻折后纸片重叠部分的面积是3cm2.
如图所示,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C,若四边形ABCD的面积为12cm2,则翻折后纸片重叠部分的面积是3cm2.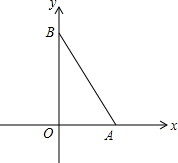 已知点A的坐标为(2,0),点B的坐标为(0,4),作等边△ABC,求点C的坐标.
已知点A的坐标为(2,0),点B的坐标为(0,4),作等边△ABC,求点C的坐标. 如图,△ABC内接于⊙O,∠A=60°,∠ABC、∠ACB的平分线交AC,AB于点D,E,CE,BD相交于点F,以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号是①③.
如图,△ABC内接于⊙O,∠A=60°,∠ABC、∠ACB的平分线交AC,AB于点D,E,CE,BD相交于点F,以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号是①③.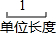 已知长度分别为3,6,2x-1的三条正整数长线段可以组成一个三角形.
已知长度分别为3,6,2x-1的三条正整数长线段可以组成一个三角形.