题目内容
4.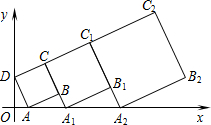 在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )| A. | 20×($\frac{3}{2}$)4030 | B. | 20×($\frac{3}{2}$)4032 | C. | 20×($\frac{3}{2}$)2016 | D. | 20×($\frac{3}{2}$)2015 |
分析 先求出正方形ABCD的边长和面积,再求出第一个正方形A1B1C1C的面积,得出规律,根据规律即可求出第2016个正方形的面积.
解答 解:∵点A的坐标为(2,0),点D的坐标为(0,4),
∴OA=2,OD=4
∵∠AOD=90°,
∴AB=AD=$\sqrt{{2}^{2}+{4}^{2}}=2\sqrt{5}$,∠ODA+∠OAD=90°,
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,S正方形ABCD=$(2\sqrt{5})^{2}$=20,
∴∠ABA1=90°,∠OAD+∠BAA1=90°,
∴∠ODA=∠BAA1,
∴△ABA1∽△DOA,
∴$\frac{B{A}_{1}}{OA}=\frac{AB}{OD}$,即$\frac{B{A}_{1}}{2}=\frac{2\sqrt{5}}{4}$,
∴BA1=$\sqrt{5}$,
∴CA1=$\frac{3\sqrt{5}}{2}$,
∴正方形A1B1C1C的面积=$(\frac{3}{2}×\sqrt{20})^{2}$=20×$(\frac{3}{2})^{2}$…,第n个正方形的面积为$20×(\frac{3}{2})^{2n-2}$,
∴第2016个正方形的面积$20×(\frac{3}{2})^{4030}$.
故选A.
点评 本题考查了正方形的性质以及坐标与图形性质;通过求出正方形ABCD和正方形A1B1C1C的面积得出规律是解决问题的关键.

练习册系列答案
相关题目
12.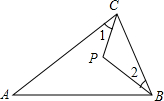 如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
 如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
9.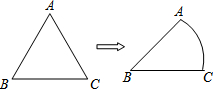 如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的$\widehat{AC}$,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )
如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的$\widehat{AC}$,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )
 如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的$\widehat{AC}$,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )
如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的$\widehat{AC}$,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )| A. | ($\frac{60}{π}$)° | B. | ($\frac{90}{π}$)° | C. | ($\frac{120}{π}$)° | D. | ($\frac{180}{π}$)° |
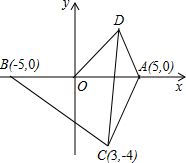 如图,在平面直角坐标系中,点A为(5,0),点B为(-5,0),点C为(3,-4),点D为第一象限上的一个动点,且OD=5.
如图,在平面直角坐标系中,点A为(5,0),点B为(-5,0),点C为(3,-4),点D为第一象限上的一个动点,且OD=5.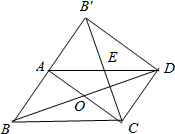 如图所示,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C,若四边形ABCD的面积为12cm2,则翻折后纸片重叠部分的面积是3cm2.
如图所示,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C,若四边形ABCD的面积为12cm2,则翻折后纸片重叠部分的面积是3cm2.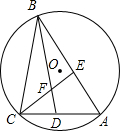 如图,△ABC内接于⊙O,∠A=60°,∠ABC、∠ACB的平分线交AC,AB于点D,E,CE,BD相交于点F,以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号是①③.
如图,△ABC内接于⊙O,∠A=60°,∠ABC、∠ACB的平分线交AC,AB于点D,E,CE,BD相交于点F,以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号是①③. 已知长度分别为3,6,2x-1的三条正整数长线段可以组成一个三角形.
已知长度分别为3,6,2x-1的三条正整数长线段可以组成一个三角形.