题目内容
17.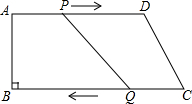 在梯形ABCD中,AD∥BC,且AD∥BC,AB=8cm,AD=20cm,BC=22cm,点P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,点Q以3cm/s的速度由C出发向B运动.
在梯形ABCD中,AD∥BC,且AD∥BC,AB=8cm,AD=20cm,BC=22cm,点P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,点Q以3cm/s的速度由C出发向B运动.(1)几秒后,四边形CDPQ为平行四边形?
(2)几秒后,PQ=CD?
分析 (1)由当PD=CQ时,四边形PQCD为平行四边形,可得方程20-2t=3t,解此方程即可求得答案;
(2)首先过D作DE⊥BC于E,可求得EC的长,又由当PQ=CD时,四边形PQCD为等腰梯形,可求得当QC-PD=QC-EF=QF+EC=2CE,即3t-(20-2t)=4时,四边形PQCD为等腰梯形,解此方程即可求得答案.再一种情况是四边形PQCD为平行四边形,PQ=CD.
解答 解:根据题意得:PA=2t,CQ=3t,则PD=AD-PA=20-2t.
(1)∵AD∥BC,
即PD∥CQ,
∴当PD=CQ时,四边形PQCD为平行四边形,
即20-2t=3t,
解得:t=4,
即当t=4时,四边形PQCD为平行四边形;
(2)由(1)得:t=4时,PQ=CD,
②过D作DE⊥BC于E,
则四边形ABED为矩形,
∴BE=AD=20cm,
∴EC=BC-BE=2cm,
当PQ=CD时,四边形PQCD为等腰梯形,如图所示:
过点P作PF⊥BC于点F,过点D作DE⊥BC于点E,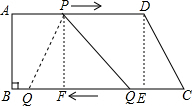
则四边形PDEF是矩形,
∴EF=PD,PF=DE,
在Rt△PQF和Rt△CDE中,
$\left\{\begin{array}{l}{PF=DE}\\{PQ=DC}\end{array}\right.$,
∴Rt△PQF≌Rt△CDE(HL),
∴QF=CE,
∴QC-PD=QC-EF=QF+EC=2CE,
即3t-(20-2t)=4,
解得:t=$\frac{24}{5}$,
即当t=$\frac{24}{5}$时,四边形PQCD为等腰梯形,PQ=DC.
综上:当t=4或$\frac{24}{5}$时,PQ=DC.
点评 此题考查了直角梯形的性质、平行四边形的判定、等腰梯形的判定以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

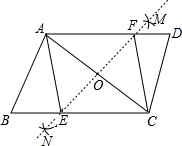 如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )
如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )| A. | AE=AF | B. | AC=EF | C. | ∠EAF=90° | D. | ∠AFE=45° |
| A. | -2,-1,0 | B. | 0,1 | C. | -1,0 | D. | 不存在 |
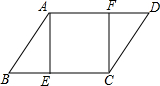 如图,在?ABCD中,∠B=60°,AB=12,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,则四边形AECF的周长为( )
如图,在?ABCD中,∠B=60°,AB=12,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,则四边形AECF的周长为( )| A. | 18 | B. | 24$\sqrt{2}$ | C. | 24 | D. | 24$\sqrt{3}$ |
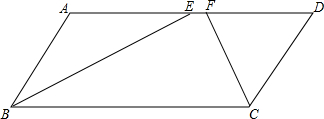 如图,在平行四边形ABCD中,∠ABC的平分线BE交边AD于点E,∠BCD的平分线CF交边AD于点F.求证:AF=DE.
如图,在平行四边形ABCD中,∠ABC的平分线BE交边AD于点E,∠BCD的平分线CF交边AD于点F.求证:AF=DE.
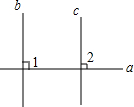 如图,已知a⊥b,a⊥c,求证:b∥c.
如图,已知a⊥b,a⊥c,求证:b∥c.