题目内容
5.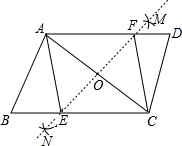 如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )
如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )| A. | AE=AF | B. | AC=EF | C. | ∠EAF=90° | D. | ∠AFE=45° |
分析 先根据题意得出直线MN是线段AC的垂直平分线,故AF=CF,AE=CE,OA=OC,再由ASA定理得出△COE≌△AOF,根据全等三角形的性质即可得出结论.
解答 解:∵在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,
∴直线MN是线段AC的垂直平分线,
∴AF=CF,AE=CE,OA=OC.
∵AE∥CE,
∴∠ECO=∠FAO,∠COE=∠AOF.
在△COE与△AOF中,
$\left\{\begin{array}{l}∠ECO=∠FAO\\ OC=OA\\∠COE=∠AOF\end{array}\right.$,
∴△COE≌△AOF(ASA),
∴AF=CE,
∴AF=AE,故A正确,B、C、D错误.
故选A.
点评 本题考查的是平行四边形的性质,涉及到线段垂直平分线的性质及全等三角形的判定与性质,根据线段垂直平分线的作法得出直线MN是线段AC的垂直平分线是解答此题的关键.

练习册系列答案
相关题目
16.反比例函数y=$\frac{k}{x}$,当自变量x的值从1增加到2,函数值就减少了3,则函数解析式为( )
| A. | y=$\frac{3}{x}$ | B. | y=$\frac{2}{x}$ | C. | y=$\frac{6}{x}$ | D. | y=3x |
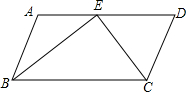 已知:平行四边形ABCD,点E在AD上,且BE平分∠ABC,CE平分∠BCD,tan∠EBC=$\frac{1}{2}$,BE=4,则△CDE的面积为$\frac{6}{5}$.
已知:平行四边形ABCD,点E在AD上,且BE平分∠ABC,CE平分∠BCD,tan∠EBC=$\frac{1}{2}$,BE=4,则△CDE的面积为$\frac{6}{5}$.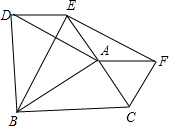 如图,分别以△ABC的三边向外作等边三角形:△ABD,△BCE,△ACF,连接DE,EF.
如图,分别以△ABC的三边向外作等边三角形:△ABD,△BCE,△ACF,连接DE,EF.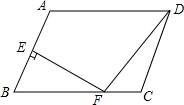 在?ABCD中,AB=6,AD=8,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为2$\sqrt{13}$.
在?ABCD中,AB=6,AD=8,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为2$\sqrt{13}$.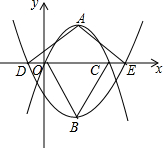 如图,在平面直角坐标系中,顶点为A的抛物线y=a1(x-2)2+2与x轴交于点O、C.顶点为B的抛物线y=a2(x-2)2-3与x轴交于点D、E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1:1.
如图,在平面直角坐标系中,顶点为A的抛物线y=a1(x-2)2+2与x轴交于点O、C.顶点为B的抛物线y=a2(x-2)2-3与x轴交于点D、E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1:1.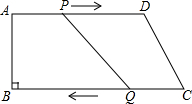 在梯形ABCD中,AD∥BC,且AD∥BC,AB=8cm,AD=20cm,BC=22cm,点P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,点Q以3cm/s的速度由C出发向B运动.
在梯形ABCD中,AD∥BC,且AD∥BC,AB=8cm,AD=20cm,BC=22cm,点P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,点Q以3cm/s的速度由C出发向B运动.