题目内容
8．
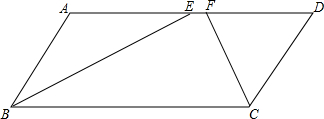如图，在平行四边形ABCD中，∠ABC的平分线BE交边AD于点E，∠BCD的平分线CF交边AD于点F．求证：AF=DE．
分析 根据平行四边形的性质得出AB=CD，AD∥BC，求出∠AEB=∠EBC，∠ABE=∠EBC，推出∠ABE=∠AEB，根据等腰三角形判定得出AB=AE，同理DF=DC，求出AE=DF即可．
解答 证明：∵四边形ABCD是平行四边形，
∴AB=CD，AD∥BC，
∴∠AEB=∠EBC，
∵BE平分∠ABC，
∴∠ABE=∠EBC，
∴∠ABE=∠AEB，
∴AB=AE，
同理DF=DC，
∴AE=DF，
∴AE+EF=DF+EF，
∴AF=DE．
点评 本题考查了平行四边形的性质，平行线的性质，等腰三角形的判定的应用，能求出AB=AE和DF=DC是解此题的关键．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
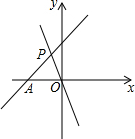如图，直线y=x+3交x轴于A，与直线y=kx交于点P，且S△AOP=3，求关于x的不等式0＜kx＜x+3的解集．
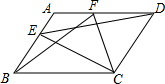如图，在平行四边形ABCD中，点E是AB边上一点，点F是AD边上一点，试说明S△ECD=S△FBC的理由．
16．反比例函数y=$\frac{k}{x}$，当自变量x的值从1增加到2，函数值就减少了3，则函数解析式为（ ）
| A． | y=$\frac{3}{x}$ | B． | y=$\frac{2}{x}$ | C． | y=$\frac{6}{x}$ | D． | y=3x |
已知?ABCD中，AE平分∠BAD交BC于点E，且BE=3，EC=2，求?ABCD的周长．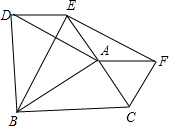
如图，分别以△ABC的三边向外作等边三角形：△ABD，△BCE，△ACF，连接DE，EF．
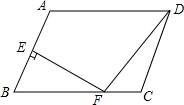在?ABCD中，AB=6，AD=8，∠ABC=60°，点E是AB的中点，EF⊥AB交BC于F，连接DF，则DF的长为2$\sqrt{13}$．
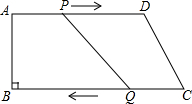在梯形ABCD中，AD∥BC，且AD∥BC，AB=8cm，AD=20cm，BC=22cm，点P、Q分别从A、C同时出发，P以2cm/s的速度由A向D运动，点Q以3cm/s的速度由C出发向B运动．