题目内容
9．
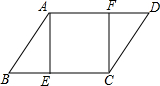如图，在?ABCD中，∠B=60°，AB=12，AE⊥BC于点E，CF⊥AD于点F，若四边形AECF是正方形，则四边形AECF的周长为（ ）| A． | 18 | B． | 24$\sqrt{2}$ | C． | 24 | D． | 24$\sqrt{3}$ |
分析 由已知条件可知直角三角形ABE可解，则AE的长可求出，进而可求出四边形AECF的周长．
解答 解：∵在?ABCD中，∠B=60°，AE⊥BC于点E，
∴∠BAE=30°，
∵AB=12，
∴BE=6，
∴AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=6$\sqrt{3}$，
∵四边形AECF是正方形，
∴四边形AECF的周长=4AE=24$\sqrt{3}$，
故选D．
点评 本题考查了正方形的性质、平行四边形的性质、含30°角的直角三角形的性质；熟练掌握正方形的性质，由正方形的性质和直角三角形的性质是解决问题的关键．
练习册系列答案
相关题目
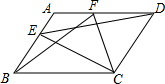如图，在平行四边形ABCD中，点E是AB边上一点，点F是AD边上一点，试说明S△ECD=S△FBC的理由．
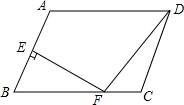在?ABCD中，AB=6，AD=8，∠ABC=60°，点E是AB的中点，EF⊥AB交BC于F，连接DF，则DF的长为2$\sqrt{13}$．
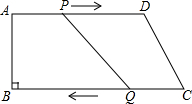在梯形ABCD中，AD∥BC，且AD∥BC，AB=8cm，AD=20cm，BC=22cm，点P、Q分别从A、C同时出发，P以2cm/s的速度由A向D运动，点Q以3cm/s的速度由C出发向B运动．
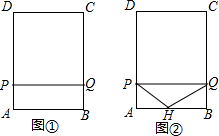如图①，在矩形ABCD中，AB=9．AD=12．点P从点A出发以每秒3个单位长度的速度沿A-D-C-B-A运动一周到点A停止．当点P不与矩形ABCD的顶点重合时，过点P作直线PQ⊥AP，与矩形的边的另一交点为Q．设点P的运动时间为t（秒）．