题目内容
7．平行四边形ABCD中三个顶点的坐标为A（2，3）、B（1，1）、C（4，2），则D的坐标为（4，4），平行四边形ABCD的面积为4．分析 画出图形即可求出点D坐标，再证明四边形ABCD是菱形，求出对角线的长即可解决问题．
解答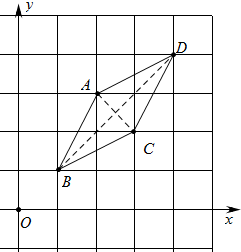 
解：如图，由图象可知点D坐标为（4，4）．
∵AB=BC=AD=CD=$\sqrt{5}$，
∴四边形ABCD是菱形，
∵AC=$\sqrt{2}$，BD=4$\sqrt{2}$，
∴四边形ABCD面积=$\frac{1}{2}$•BD•AC=$\frac{1}{2}$$•4\sqrt{2}$$•\sqrt{2}$=4．
故答案分别为（4，4），4．
点评 本题考查平行四边形的性质、菱形的判定和性质、勾股定理等知识，解题的关键是正确画出图形，记住菱形的面积公式=对角线乘积的一半，属于中考常考题型．
练习册系列答案
相关题目
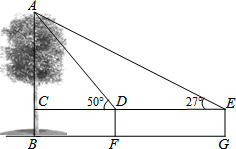某数学兴趣小组用高为1.2米的测角仪测量小树AB的高度，如图，在距AB一定距离的F处测得小树顶部A的仰角为50°，沿BF方向行走3.5米到G处时，又测得小树顶部A的仰角为27°，求小树AB的高度．（参考数据：sin27°=0.45，cos27°=0.89，tan27°=0.5，sin50°=0.77，cos50°=0.64，tan50°=1.2）
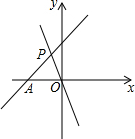如图，直线y=x+3交x轴于A，与直线y=kx交于点P，且S△AOP=3，求关于x的不等式0＜kx＜x+3的解集．
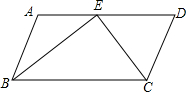已知：平行四边形ABCD，点E在AD上，且BE平分∠ABC，CE平分∠BCD，tan∠EBC=$\frac{1}{2}$，BE=4，则△CDE的面积为$\frac{6}{5}$．
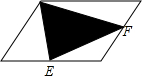已知平行四边形的面积是128平方厘米，E、F分别是两条边上的中点，求阴影部分的面积．
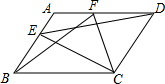如图，在平行四边形ABCD中，点E是AB边上一点，点F是AD边上一点，试说明S△ECD=S△FBC的理由．
16．反比例函数y=$\frac{k}{x}$，当自变量x的值从1增加到2，函数值就减少了3，则函数解析式为（ ）
| A． | y=$\frac{3}{x}$ | B． | y=$\frac{2}{x}$ | C． | y=$\frac{6}{x}$ | D． | y=3x |
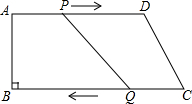在梯形ABCD中，AD∥BC，且AD∥BC，AB=8cm，AD=20cm，BC=22cm，点P、Q分别从A、C同时出发，P以2cm/s的速度由A向D运动，点Q以3cm/s的速度由C出发向B运动．