题目内容
7.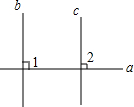 如图,已知a⊥b,a⊥c,求证:b∥c.
如图,已知a⊥b,a⊥c,求证:b∥c.
分析 首先根据垂直定义可得∠1=∠2=90°,再根据平行线的判定进而证明即可.
解答 证明:∵a⊥b,a⊥c,
∴∠1=∠2=90°,
∴b∥c(同位角相等,两直线平行).
点评 此题主要考查了平行线的判定,以及垂直定义,关键是掌握同位角相等,两直线平行.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.若线段AB的端点坐标分别为A(-2,3),B(0,5),将它向下平移5个单位,则其端点坐标变为( )
| A. | A′(3,3),B′(0,0) | B. | A′(-2,-2),B′(0,0) | C. | A′(3,3),B′(5,5) | D. | A′(3,3),B′(-5,5) |
17.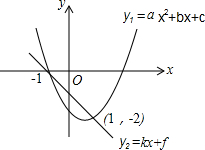 若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )
若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )
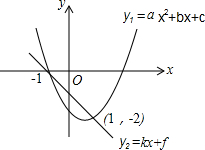 若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )
若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )| A. | $\left\{\begin{array}{l}{mx<1}\\{nx>1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{mx>1}\\{nx>1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{mx>1}\\{nx<1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{mx<1}\\{nx<1}\end{array}\right.$ |
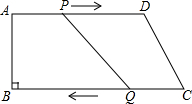 在梯形ABCD中,AD∥BC,且AD∥BC,AB=8cm,AD=20cm,BC=22cm,点P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,点Q以3cm/s的速度由C出发向B运动.
在梯形ABCD中,AD∥BC,且AD∥BC,AB=8cm,AD=20cm,BC=22cm,点P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,点Q以3cm/s的速度由C出发向B运动.