题目内容
6.先化简,再求值:($\frac{3x}{x+1}-\frac{x}{x-1})÷\frac{x-2}{{x}^{2}-1}$÷$\frac{x-2}{{x}^{2}-1}$,其中x=$\frac{1}{1-\sqrt{3}}$.分析 先算括号里面的,再算除法,分式化为最简根式后,把x的值代入进行计算即可.
解答 解:原式=$\frac{3x(x-1)-x(x+1)}{(x+1)(x-1)}$•$\frac{(x+1)(x-1)}{x-2}$
=$\frac{3{x}^{2}-3x-{x}^{2}-x}{(x+1)(x-1)}$•$\frac{(x+1)(x-1)}{x-2}$
=$\frac{2x(x-2)}{(x+1)(x-1)}$•$\frac{(x+1)(x-1)}{x-2}$
=2x,
当x=$\frac{1}{1-\sqrt{3}}$时,原式=$\frac{2}{1-\sqrt{3}}$=-1-$\sqrt{3}$.
点评 本题考查的是整式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.反比例函数y=$\frac{k}{x}$,当自变量x的值从1增加到2,函数值就减少了3,则函数解析式为( )
| A. | y=$\frac{3}{x}$ | B. | y=$\frac{2}{x}$ | C. | y=$\frac{6}{x}$ | D. | y=3x |
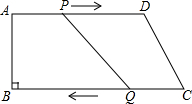 在梯形ABCD中,AD∥BC,且AD∥BC,AB=8cm,AD=20cm,BC=22cm,点P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,点Q以3cm/s的速度由C出发向B运动.
在梯形ABCD中,AD∥BC,且AD∥BC,AB=8cm,AD=20cm,BC=22cm,点P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,点Q以3cm/s的速度由C出发向B运动.