题目内容
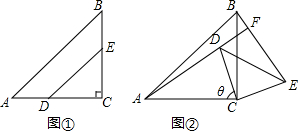
12.如图①,在△ABC中,∠ACB=90°,AC=BC,在AC、BC边上分别截取CD=CE,连结DE.将△DCE绕着点C顺时针旋转θ角,连结BE、AD.(1)当0°<θ<90°时,如图②,直线BE交直线AD于点F.
①求证:△ACD≌△BCE.
②求证:AF⊥BE.
(2)当0°<θ<360°,AC=5,CD=3,四边形CDFE是正方形时,直接写出AF的长度.
分析 (1)①根据旋转的性质和已知,运用SAS证明即可;②由问题原型中的结论:△ACE≌△BCE得出∠BFO=∠ACB,结合等量代换进行求解即可;
(2)运用CD∥BE结合初步探究中的结论,可证CD⊥AF,结合勾股定理即可求解.
解答 解:(1)①如图②,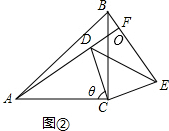
∵△DCE绕着点C顺时针旋转θ角,由旋转的性质可知,
∴∠ACD=∠BCE=θ,
又∵AC=BC,CD=CE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE;
②如图②,设AF与BC交点于O,
∵△ACD≌△BCE,
∴∠DAC=∠EBC,
∵∠AOC=∠BOF,
∴∠BFO=∠ACB=90°,
∴AF⊥BE;
(2)如图③,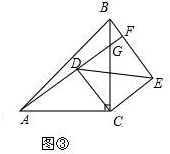
∵AC=5,CD=3,四边形CDFE是正方形时,
∵AD⊥CD,
∴AD=$\sqrt{{5}^{2}-{3}^{2}}=4$,
∴AF=4+3=7,
如图4,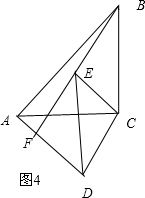
∴AF=4-3=1.
点评 此题主要考查几何变换中的旋转,熟悉旋转的性质,会证明三角形全等,并应用全等三角形的性质解决角的问题,会运用勾股定理求线段长度是解题的关键.

练习册系列答案
相关题目
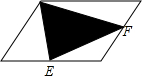 已知平行四边形的面积是128平方厘米,E、F分别是两条边上的中点,求阴影部分的面积.
已知平行四边形的面积是128平方厘米,E、F分别是两条边上的中点,求阴影部分的面积. 已知?ABCD中,AE平分∠BAD交BC于点E,且BE=3,EC=2,求?ABCD的周长.
已知?ABCD中,AE平分∠BAD交BC于点E,且BE=3,EC=2,求?ABCD的周长.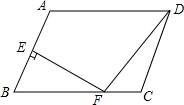 在?ABCD中,AB=6,AD=8,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为2$\sqrt{13}$.
在?ABCD中,AB=6,AD=8,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为2$\sqrt{13}$. 如图,已知在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60°,CE=3cm,FC=1cm,求AB,BC的长及ABCD面积.
如图,已知在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60°,CE=3cm,FC=1cm,求AB,BC的长及ABCD面积.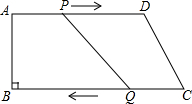 在梯形ABCD中,AD∥BC,且AD∥BC,AB=8cm,AD=20cm,BC=22cm,点P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,点Q以3cm/s的速度由C出发向B运动.
在梯形ABCD中,AD∥BC,且AD∥BC,AB=8cm,AD=20cm,BC=22cm,点P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,点Q以3cm/s的速度由C出发向B运动.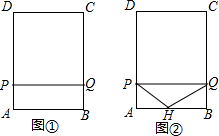 如图①,在矩形ABCD中,AB=9.AD=12.点P从点A出发以每秒3个单位长度的速度沿A-D-C-B-A运动一周到点A停止.当点P不与矩形ABCD的顶点重合时,过点P作直线PQ⊥AP,与矩形的边的另一交点为Q.设点P的运动时间为t(秒).
如图①,在矩形ABCD中,AB=9.AD=12.点P从点A出发以每秒3个单位长度的速度沿A-D-C-B-A运动一周到点A停止.当点P不与矩形ABCD的顶点重合时,过点P作直线PQ⊥AP,与矩形的边的另一交点为Q.设点P的运动时间为t(秒).