方程x2-2$\sqrt{3}$x+3=0的根是( )A．x=$\sqrt{3}$B．x1=x2=$\sqrt{3}$C．x=3D．x1=x2=3 题目和参考答案——青夏教育精英家教网—

题目内容

15．方程x²-2$\sqrt{3}$x+3=0的根是（　　）

A．

x=$\sqrt{3}$

B．

x₁=x₂=$\sqrt{3}$

C．

x=3

D．

x₁=x₂=3

分析根据完全平方公式可得（x-$\sqrt{3}$）²=0，即可得答案．

解答解：x²-2$\sqrt{3}$x+3=0，即x²-2$\sqrt{3}$x+（$\sqrt{3}$）²=0，
（x-$\sqrt{3}$）²=0，
∴x₁=x₂=$\sqrt{3}$，
故选：B

点评本题主要考查一元二次方程的解法，熟练掌握完全平方公式是解题的关键．

练习册系列答案

相关题目

5．

如图是用一张长方形纸片折成的，如果∠1=100°，那么∠2的度数是（　　）

6．如图所示，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫格点，以格点为顶点分别按下列要求画三角形．
（1）使三角形的三边长分别为3，2$\sqrt{2}$，$\sqrt{5}$（在图①中画一个即可）；
（2）使三角形为钝角三角形，且面积为4（在图②中画一个即可）．

3．

如图，点P在∠AOB内，点M，N分别是点P关于AO，BO的对称点，若△PEF的周长等于20cm，则MN的长为20cm．

10．数学问题：计算数列8，5，2，…前n项的和．
探究问题：为解决上面的问题，我们从最简单的问题进行探究．
探究一：首先我们来认识什么是等差数列．
数学上，称按一定顺序排列的一列数为数列，其中排在第一位的数称为第一项，用a₁表示；排在第二位的数称为第二项，用a₂表示；…：排在第n位的数称为第n项，用a_n表示，并称a_n为数列的通项，如果一个数列从第二项起，每一项与它的前一项的差都等于同一个常数，那么这个数叫做等差数列，这个常数叫等差数列的公差，公差通常用d表示．
（1）根据以上表述：可得：a₂=a₁+d，a₃=a₁+2d，a₄=a₁+3d，…；
则通项a_n=a₁+（n-1）d；
（2）已知数列8，5，2，…为等差数列，请判断-100是否是此等差数列的某一项，若是，请求出是第几项；若不是，说明理由；
探究二：200多年前，数学王子高斯用他独特的方法快速计算出1+2+3+…+100的值．我们从这个算法中受到启发，用先方法计算数列1，2，3，…，n₀…的前n项和；
由$\frac{\left.\begin{array}{l}{1+2+…+n-1+n}\\{n+n-1+…+2+1}\end{array}\right.}{（n+1）（n+1）+…+（n+1）+（n+1）}$可知1+2+3+…+n=$\frac{（n+1）×n}{2}$．
（3）请你仿照上面的探究方式，解决下面的问题：
若a₁，a₂，a₃…，a_n为等差数列的前n项，前n项和S_n=a₁+a₂+a₃+…+a_n
证明：S_n=na₁+$\frac{n（n-1）}{2}$d．
解决问题：（4）计算：数列8，5，2，…前n项的和S_n（写出计算过程）．

20．

如图，在△ABC中，直线MN为BC的垂直平分线，交BC于点E，点D在直线MN上，且在△ABC的外面，连接BD，CD，若CA平分∠BCD，∠A=65°，∠ABC=85°，则△BCD是（　　）

7．计算：$-2a（\frac{1}{2}{a^2}b+b）$=-a³b-2ab．

4．命题“全等三角形的对应角相等”的逆命题是对应角相等的三角形是全等三角形，它是假命题（填真或假）

6．

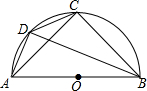如图，AB是半圆O的直径，点C是$\widehat{AB}$的中点，D是$\widehat{AC}$上一点，且BD-AD=$\sqrt{2}$，则弦CD的长为（　　）

A．

$\sqrt{2}$

B．

$\frac{1}{2}\sqrt{2}$

C．

D．

$\frac{1}{2}$

试题分类