题目内容
14.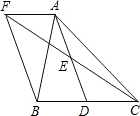 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)BD与CD有什么数量关系,并说明理由;
(2)当AB=AC时,试判断四边形AFBD是什么四边形?说明理由.
分析 (1)先由AF∥BC,利用平行线的性质可证∠AFE=∠DCE,而E是AD中点,那么AE=DE,∠AEF=∠DEC,利用AAS可证△AEF≌△DEC,那么有AF=DC,又AF=BD,从而有BD=CD;
(2)四边形AFBD是矩形.由于AF平行等于BD,易得四边形AFBD是平行四边形,又AB=AC,BD=CD,利用等腰三角形三线合一定理,可知AD⊥BC,即∠ADB=90°,那么可证四边形AFBD是矩形.
解答 解:BD=CD,
理由:
(1)∵AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
$\left\{\begin{array}{l}{∠AFE=∠DCE}\\{AE=DE}\\{∠AEF=∠DEC}\end{array}\right.$,
∴△AEF≌△DEC(AAS),
∴AF=DC,
∵AF=BD,
∴BD=CD;
(2)四边形AFBD是矩形.
理由:
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴∠ADB=90°
∵AF=BD,
∵过A点作BC的平行线交CE的延长线于点F,即AF∥BC,
∴四边形AFBD是平行四边形,
又∵∠ADB=90°,
∴四边形AFBD是矩形.
点评 本题利用了平行线的性质、全等三角形的判定和性质、等量代换、平行四边形的判定、等腰三角形三线合一定理、矩形的判定等知识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知-x+y=3,则2(x-y)2-4(x-y)+6的值是( )
| A. | 9 | B. | 12 | C. | -15 | D. | 36 |
2.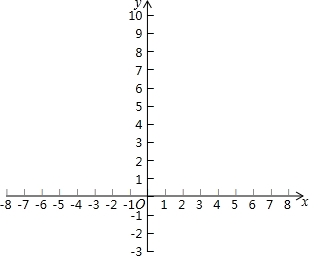 有这样一个问题:探究函数$y=\frac{x}{x+1}$的图象与性质.小怀根据学习函数的经验,对函数$y=\frac{x}{x+1}$的图象与性质进行了探究.下面是小怀的探究过程,请补充完成:
有这样一个问题:探究函数$y=\frac{x}{x+1}$的图象与性质.小怀根据学习函数的经验,对函数$y=\frac{x}{x+1}$的图象与性质进行了探究.下面是小怀的探究过程,请补充完成:
(1)函数$y=\frac{x}{x+1}$的自变量x的取值范围是x≠-1;
(2)列出y与x的几组对应值.请直接写出m的值,m=3;
(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出函数$y=\frac{x}{x+1}$的一条性质.
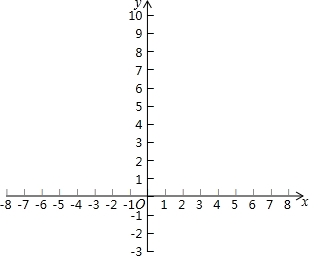 有这样一个问题:探究函数$y=\frac{x}{x+1}$的图象与性质.小怀根据学习函数的经验,对函数$y=\frac{x}{x+1}$的图象与性质进行了探究.下面是小怀的探究过程,请补充完成:
有这样一个问题:探究函数$y=\frac{x}{x+1}$的图象与性质.小怀根据学习函数的经验,对函数$y=\frac{x}{x+1}$的图象与性质进行了探究.下面是小怀的探究过程,请补充完成:(1)函数$y=\frac{x}{x+1}$的自变量x的取值范围是x≠-1;
(2)列出y与x的几组对应值.请直接写出m的值,m=3;
(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出函数$y=\frac{x}{x+1}$的一条性质.
| x | … | -5 | -4 | -3 | -2 | -$\frac{3}{2}$ | -$\frac{1}{2}$ | 0 | 1 | 2 | m | 4 | 5 | … |
| y | … | $\frac{5}{4}$ | $\frac{4}{3}$ | $\frac{3}{2}$ | 2 | 3 | -1 | 0 | $\frac{1}{2}$ | $\frac{2}{3}$ | $\frac{3}{4}$ | $\frac{4}{5}$ | $\frac{5}{6}$ | … |
19.下列线段中,不可能是同一个三角形的三边上的高的是( )
| A. | 1cm,1cm,2cm | B. | 2cm,2cm,1cm | C. | 2cm,3cm,3cm | D. | 3cm,4cm,6cm |
6.若x-1=2(y+1)=3(z+2),则x2+y2+z2可取得的最小值为( )
| A. | 6 | B. | $\frac{41}{7}$ | C. | $\frac{83}{14}$ | D. | $\frac{293}{49}$ |
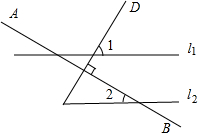 如图,直线l1∥l2,AB⊥CD,∠1=56.5°,那么∠2=33.5°.
如图,直线l1∥l2,AB⊥CD,∠1=56.5°,那么∠2=33.5°.