题目内容
1.若x+$\sqrt{{x}^{2}-1}$+$\frac{1}{x-\sqrt{{x}^{2}-1}}$=10,求x2+$\sqrt{{x}^{4}-1}$+$\frac{1}{{x}^{2}+\sqrt{{x}^{4}-1}}$的值.分析 根据x+$\sqrt{{x}^{2}-1}$+$\frac{1}{x-\sqrt{{x}^{2}-1}}$=10,化简可以求得x的值,再将所求的式子化简,将x的值代入即可解答本题.
解答 解:∵x+$\sqrt{{x}^{2}-1}$+$\frac{1}{x-\sqrt{{x}^{2}-1}}$=10,
∴$x+\sqrt{{x}^{2}-1}+\frac{x+\sqrt{{x}^{2}-1}}{(x-\sqrt{{x}^{2}-1})(x+\sqrt{{x}^{2}-1})}$=10
化简,得$x+\sqrt{{x}^{2}-1}=5$,
解得,x=2.6
∴x2+$\sqrt{{x}^{4}-1}$+$\frac{1}{{x}^{2}+\sqrt{{x}^{4}-1}}$
=${x}^{2}+\sqrt{{x}^{4}-1}+\frac{{x}^{2}-\sqrt{{x}^{4}-1}}{({x}^{2}+\sqrt{{x}^{4}-1})({x}^{2}-\sqrt{{x}^{4}-1})}$
=${x}^{2}+\sqrt{{x}^{4}-1}+{x}^{2}-\sqrt{{x}^{4}-1}$
=2x2
=2×2.62
=2×6.76
=13.52.
即x2+$\sqrt{{x}^{4}-1}$+$\frac{1}{{x}^{2}+\sqrt{{x}^{4}-1}}$的值是13.52.
点评 本题考查二次根式的化简求值,解题的关键是对题目中的式子和所求的式子进行分母有理化,然后进行化简求值.

练习册系列答案
相关题目
11.抛物线$y=-{(x-\frac{1}{2})^2}$+3的对称轴是( )
| A. | 直线$x=-\frac{1}{2}$ | B. | 直线$x=\frac{1}{2}$ | C. | 直线x=3 | D. | 直线x=-3 |
 如图所示,△ABC的顶点都在小正方形的顶点上,在方格纸上画出所有与△ABC全等且仅有1条公共边的格点三角形.
如图所示,△ABC的顶点都在小正方形的顶点上,在方格纸上画出所有与△ABC全等且仅有1条公共边的格点三角形.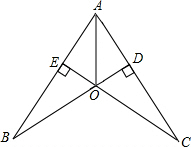 已知:如图,CE⊥AB于点E,BD⊥AC于点D,BD,CE交于点O,且BO=CO,求证:O在∠BAC的角平分线上.
已知:如图,CE⊥AB于点E,BD⊥AC于点D,BD,CE交于点O,且BO=CO,求证:O在∠BAC的角平分线上.