题目内容
11.抛物线$y=-{(x-\frac{1}{2})^2}$+3的对称轴是( )| A. | 直线$x=-\frac{1}{2}$ | B. | 直线$x=\frac{1}{2}$ | C. | 直线x=3 | D. | 直线x=-3 |
分析 直接利用抛物线顶点式的特殊形式即可求得对称轴.
解答 解:∵y=-(x-$\frac{1}{2}$)2+3
∴其对称轴为x=$\frac{1}{2}$,
故选B.
点评 本题考查了二次函数的性质,求抛物线的对称轴和顶点坐标的方法是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
19.下列图形中不一定是轴对称图形的是( )
| A. | 角 | B. | 平行四边形 | C. | 等腰三角形 | D. | 正方形 |
16.若a>b,则不等式组$\left\{\begin{array}{l}{x<a+1}\\{x<b+1}\end{array}\right.$的解集是( )
| A. | x<a+1 | B. | x<b+1 | C. | b+1<x<a+1 | D. | b<x<a |
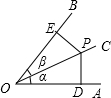 如图,设∠AOC=α,∠BOC=β,P为射线OC上一点,PD⊥OA于D,PE⊥OB于E,则$\frac{PD}{PE}$等于$\frac{sinα}{sinβ}$ (用α、β的三角函数表示)
如图,设∠AOC=α,∠BOC=β,P为射线OC上一点,PD⊥OA于D,PE⊥OB于E,则$\frac{PD}{PE}$等于$\frac{sinα}{sinβ}$ (用α、β的三角函数表示) 如图,AD∥BC,∠A=2∠ABC,BD平分∠ABC,求∠ADB的度数.
如图,AD∥BC,∠A=2∠ABC,BD平分∠ABC,求∠ADB的度数.