题目内容
6.某车间有甲、乙两名组装工人,乙工人由于采用了新式组装工具,其工作效率比甲工人高20%,完成30台机器的组装工作,乙工人比甲工人少用1小时.(1)求甲、乙两名组装工人每小时各完成多少台机器的组装;
(2)现在需要这两名工人合作组装44台机器,应如何分配组装任务,才能让两名工人同时完成任务?
分析 (1)设甲工人每小时完成x台机器的组装,则乙工人每小时完成(1+20%)x台机器的组装,根据完成30台机器的组装工作,乙工人比甲工人少用1小时列出方程解答即可;
(2)根据(1)中求得的数据,设甲组装a台,则乙组装(44-a)台,根据所用时间相等列出方程解答即可.
解答 解:(1)设甲工人每小时完成x台机器的组装,由题意得
$\frac{30}{x}$-1=$\frac{30}{(1+20%)x}$
解得:x=5,
经检验x=5是原分式方程的解,
则(1+20%)x=6
答:甲工人每小时完成5台机器的组装,乙工人每小时完成6台机器的组装.
(2)设甲组装a台,则乙组装(44-a)台,由题意得
$\frac{a}{5}$=$\frac{44-a}{6}$
解得:a=20
44-a=24
答:甲组装20台,乙组装24台,才能让两名工人同时完成任务.
点评 此题考查分式方程的实际运用,一元一次方程的实际运用,找出题目蕴含的数量关系是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.若a>b,则不等式组$\left\{\begin{array}{l}{x<a+1}\\{x<b+1}\end{array}\right.$的解集是( )
| A. | x<a+1 | B. | x<b+1 | C. | b+1<x<a+1 | D. | b<x<a |
14.已知等边△ABC中,A(-1,0),B(5,0),则点C的坐标为( )
| A. | (2,3$\sqrt{3}$) | B. | (2,-3$\sqrt{3}$) | C. | (3$\sqrt{3}$,2) | D. | (2,3$\sqrt{3}$)或(2,-3$\sqrt{3}$) |
 如图,AD是△ABC的中线,AE⊥AC,AF⊥AB,且AE=AC,AF=AB,求证:AD=$\frac{1}{2}$EF.
如图,AD是△ABC的中线,AE⊥AC,AF⊥AB,且AE=AC,AF=AB,求证:AD=$\frac{1}{2}$EF.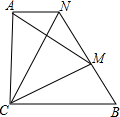 如图,点M在BN上,△ACM、△CBN是等边三角形,试证明:(1)AN=BM;(2)AN+MN=CN;(3)AN∥BC.
如图,点M在BN上,△ACM、△CBN是等边三角形,试证明:(1)AN=BM;(2)AN+MN=CN;(3)AN∥BC.