题目内容
19．
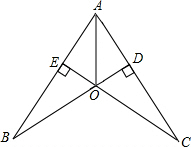已知：如图，CE⊥AB于点E，BD⊥AC于点D，BD，CE交于点O，且BO=CO，求证：O在∠BAC的角平分线上．
分析 先证明△BOE≌△COD，得出OD=OE，证出点O在∠BAC的平分线上即可．
解答 证明：∵CD⊥AB，BE⊥AC，
∴∠BEO=∠CDO=90°，
在△BOE和△COD中，
$\left\{\begin{array}{l}{∠BEO=∠CDO}&{\;}\\{∠BOE=∠COD}&{\;}\\{BO=CO}&{\;}\end{array}\right.$，
∴△BED≌△COD（AAS），
∴OE=OD，
∴点O在∠BAC的平分线上．
点评 本题考查了全等三角形的判定与性质以及角的平分线的判定；证明三角形全等得出OE=OD是解决问题的关键．
练习册系列答案
相关题目
如图，AD是△ABC的中线，AE⊥AC，AF⊥AB，且AE=AC，AF=AB，求证：AD=$\frac{1}{2}$EF．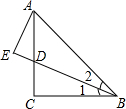
如图，△ABC是等腰直角三角形，AC=BC，∠C=90°，AE⊥BD，AE=$\frac{1}{2}$BD．求证：∠1=∠2．
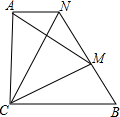如图，点M在BN上，△ACM、△CBN是等边三角形，试证明：（1）AN=BM；（2）AN+MN=CN；（3）AN∥BC．
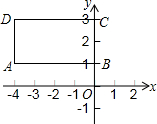如图所示，在长方形ABCDA中，A（-4，1），B（0，1），C（0，3）．