题目内容
3.为了认真贯彻教育部关于与开展“阳光体育”活动的文件精神,实施全国亿万学生每天集体锻炼一小时活动,吸引同学们走向操场、走进大自然、走到阳光下,积极参加体育锻炼,掀起校园内体育锻炼热潮,我市各学校结合实际情况举办了“阳光体育”系列活动,为了解“阳光体育”活动的落实情况,我市教育部门在红旗中学2000名学生中,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的活动),并将调查结果绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)参加调查的人数共有300人,在扇形统计图中,表示“C”的扇形的圆心角为108度;
(2)补全条形统计图,并计算扇形统计图中m的值;
(3)若要从该校喜欢“D”项目的学生中随机选择8名进行节目排练,则喜欢该项目的小丽同学被选中的概率是多少?
分析 (1)用喜欢乒乓球的人数除以其所占的百分比即可求得调查的总人数,;
(2)用喜欢C项目的人数除以总人数即可求得其百分率,从而得到m的值;
(3)利用概率公式即可求得该同学被抽中的概率.
解答 解:(1)参加调查的人数为69÷23%=300(人),
∵“C”的人数为:300-60-69-36-45=90(人),
∴表示“C”的扇形的圆心角为$\frac{90}{300}$×360°=108°,
故答案为:300,108.
(2)补全条形图如下:
∵m%=$\frac{60}{300}$×100%=20%,
∴m=20;
(3)$\frac{8}{36}$=$\frac{2}{9}$,
答:喜欢该项目的小丽同学被选中的概率是$\frac{2}{9}$.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小,也考查了概率公式的应用.

练习册系列答案
相关题目
18. 2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m=6,n=20%;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
 2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.| 队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 七年级 | 6.7 | m | 3.41 | 90% | n |
| 八年级 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(2)直接写出表中的m=6,n=20%;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
8. 如图,在边长为4的菱形ABCD中,∠BAD=120°,则对角线AC的长为( )
如图,在边长为4的菱形ABCD中,∠BAD=120°,则对角线AC的长为( )
 如图,在边长为4的菱形ABCD中,∠BAD=120°,则对角线AC的长为( )
如图,在边长为4的菱形ABCD中,∠BAD=120°,则对角线AC的长为( )| A. | 4 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3 |




 阅读下列材料:
阅读下列材料: 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.现将它的图形放在如图所示的直角坐标系中.求这条抛物线的解析式.
有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.现将它的图形放在如图所示的直角坐标系中.求这条抛物线的解析式. 某地区教育部门为了了解本地九年级学生每周“阳光体育活动”的时间情况,随机调査了本地部分九年级学生,把收集到的数据进行整理并制成了以下两幅统汁图.学生“阳光体育活动”的时间x(h)分为五个等级:A(x≤4),B(4<x≤6),C(6<x≤8),D(8<x≤l0>,E(x>10).
某地区教育部门为了了解本地九年级学生每周“阳光体育活动”的时间情况,随机调査了本地部分九年级学生,把收集到的数据进行整理并制成了以下两幅统汁图.学生“阳光体育活动”的时间x(h)分为五个等级:A(x≤4),B(4<x≤6),C(6<x≤8),D(8<x≤l0>,E(x>10).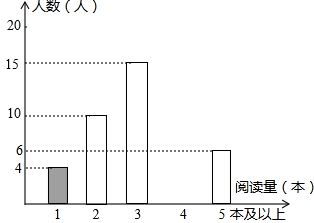 某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题:
某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题: