题目内容
11. 阅读下列材料:
阅读下列材料:在学习完锐角三角函数后,老师提出一个这样的问题:如图1,在Rt△ABC中,∠ACB=90°,AB=1,∠A=α,求sin2α(用含sinα,cosα的式子表示).
聪明的小雯同学是这样考虑的:如图2,取AB的中点O,连接OC,过点C作CD⊥AB于点D,则∠COB=2α,然后利用锐角三角函数在Rt△ABC中表示出AC,BC,在Rt△ACD中表示出CD,则可以求出
sin2α=$\frac{CD}{OC}$=$\frac{sinα•AC}{{\frac{1}{2}}}$=$\frac{sinα•cosα}{{\frac{1}{2}}}$=2sinα•cosα.
阅读以上内容,回答下列问题:
在Rt△ABC中,∠C=90°,AB=1.
(1)如图3,若BC=$\frac{1}{3}$,则 sinα=$\frac{1}{3}$,sin2α=$\frac{4\sqrt{2}}{9}$;
(2)请你参考阅读材料中的推导思路,求出tan2α的表达式(用含sinα,cosα的式子表示).
分析 (1)根据三角函数进行解答即可;
(2)利用直角三角形中的三角函数解答即可.
解答 解:(1)sinα=$\frac{1}{3}$,cosα=$\frac{2\sqrt{2}}{3}$,可得:sin2α=$\frac{{4\sqrt{2}}}{9}$;
故答案为:$\frac{1}{3}$;$\frac{4\sqrt{2}}{9}$
(2)∵AC=cosα,BC=sinα,
∴CD=$\frac{AC×BC}{AB}$=sinα•cosα.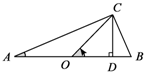
∵∠DCB=∠A,
∴在Rt△BCD中,BD=sin2α.
∴OD=$\frac{1}{2}$-sin2α.
∴tan2α=$\frac{CD}{OD}$=$\frac{sinα•cosα}{\frac{1}{2}-si{n}^{2}α}=\frac{2sinα•cosα}{1-2si{n}^{2}α}$.
点评 本题通过题目提供信息考查了解直角三角形,读懂题目信息并根据信息表示出三角形的三角函数是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
19.化简$\frac{16-{a}^{2}}{{a}^{2}+4a+4}$÷$\frac{a-4}{2a+4}$•$\frac{a-2}{a+4}$,其结果是( )
| A. | -2 | B. | 2 | C. | -$\frac{2(a-2)}{a+2}$ | D. | $\frac{2}{(a+2)^{2}}$ |
16. 如图,l1∥l2∥l3,BC=1,$\frac{DF}{EF}$=3,则AB长为( )
如图,l1∥l2∥l3,BC=1,$\frac{DF}{EF}$=3,则AB长为( )
 如图,l1∥l2∥l3,BC=1,$\frac{DF}{EF}$=3,则AB长为( )
如图,l1∥l2∥l3,BC=1,$\frac{DF}{EF}$=3,则AB长为( )| A. | 4 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
1. 如图,下列条件中,能判定DE∥AC的是( )
如图,下列条件中,能判定DE∥AC的是( )
 如图,下列条件中,能判定DE∥AC的是( )
如图,下列条件中,能判定DE∥AC的是( )| A. | ∠BED=∠EFC | B. | ∠1=∠2 | C. | ∠BEF+∠B=180° | D. | ∠3=∠4 |
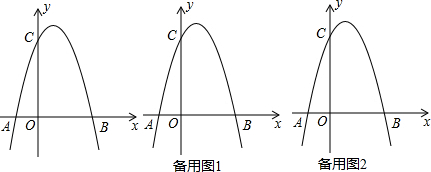
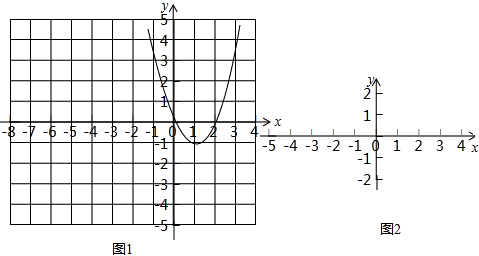 在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2,若在图形W1和W2上分别存在点M (x1,y1 )和N (x2,y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$
在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2,若在图形W1和W2上分别存在点M (x1,y1 )和N (x2,y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$