题目内容
8.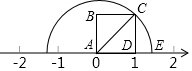 如图,四边形ABCD是正方形,点E表示的数是$\sqrt{2}$.
如图,四边形ABCD是正方形,点E表示的数是$\sqrt{2}$.
分析 根据勾股定理,可得AC的长,根据数轴上两点间的距离,可得答案.
解答 解:AC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
AE=AC=$\sqrt{2}$,
点E表示的数是$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查了实数与数轴,利用勾股定理得出AC的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3. 如图,已知AB∥CD,∠2=2∠1,则∠3=( )
如图,已知AB∥CD,∠2=2∠1,则∠3=( )
 如图,已知AB∥CD,∠2=2∠1,则∠3=( )
如图,已知AB∥CD,∠2=2∠1,则∠3=( )| A. | 90° | B. | 120° | C. | 60° | D. | 15 |
17.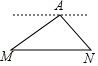 如图,在海拔200米的小山顶A处,观察M,N两地,俯角分别为30°,45°,则M,N两地的距离为( )
如图,在海拔200米的小山顶A处,观察M,N两地,俯角分别为30°,45°,则M,N两地的距离为( )
 如图,在海拔200米的小山顶A处,观察M,N两地,俯角分别为30°,45°,则M,N两地的距离为( )
如图,在海拔200米的小山顶A处,观察M,N两地,俯角分别为30°,45°,则M,N两地的距离为( )| A. | 200米 | B. | 200$\sqrt{3}$米 | C. | 400米 | D. | 200($\sqrt{3}+1$)米 |
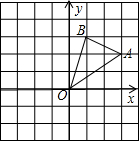 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,2),B(1,3)
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,2),B(1,3)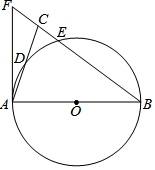 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于D、E两点,BC的延长线与⊙O的切线AF交于点F,连接BD.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于D、E两点,BC的延长线与⊙O的切线AF交于点F,连接BD.