题目内容
17.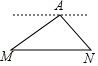 如图,在海拔200米的小山顶A处,观察M,N两地,俯角分别为30°,45°,则M,N两地的距离为( )
如图,在海拔200米的小山顶A处,观察M,N两地,俯角分别为30°,45°,则M,N两地的距离为( )| A. | 200米 | B. | 200$\sqrt{3}$米 | C. | 400米 | D. | 200($\sqrt{3}+1$)米 |
分析 分别在Rt△ABM,Rt△ABN中求出BM,BN即可解决问题.
解答  解:过A作AB⊥MN于B,在Rt△ABM中,∵∠ABM=90°,AB=200,∠M=30°,
解:过A作AB⊥MN于B,在Rt△ABM中,∵∠ABM=90°,AB=200,∠M=30°,
∴tanM=$\frac{AB}{BM}$,
∴BM=200$\sqrt{3}$,
在Rt△ABN中,∵∠ABN=90°,∠N=∠BAN=45°,
∴BN=AB=200,
∴MN=200$\sqrt{3}$+200=200($\sqrt{3}$+1)米.
故选D.
点评 本题考查解直角三角形的应用、俯角俯角、三角函数等知识,解题的关键是记住三角函数的定义,以及特殊三角形的边角关系,属于中考常考题型.

练习册系列答案
相关题目
7.在平面直角坐标系中,点A(-1,4)关于坐标原点O对称点A′的坐标是( )
| A. | (1,4) | B. | (-1,-4) | C. | (4,-1) | D. | (1,-4) |
5.计算:1+(-2)+(+3)+(-4)+(+5)+(-6)…(+99)+(-100)的结果是( )
| A. | 0 | B. | -1 | C. | -50 | D. | 51 |
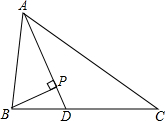 如图,△ABC中,AD平分∠BAC,BP⊥AD于点P,AB=5,BP=1,AC=9,说明∠ABP=2∠ACB的理由.
如图,△ABC中,AD平分∠BAC,BP⊥AD于点P,AB=5,BP=1,AC=9,说明∠ABP=2∠ACB的理由.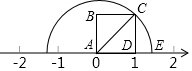 如图,四边形ABCD是正方形,点E表示的数是$\sqrt{2}$.
如图,四边形ABCD是正方形,点E表示的数是$\sqrt{2}$. 如图,二次函数y=ax2+bx+2的图象与x轴交于点A(-1,0)、B(4,0),与y轴正半轴交于点C.
如图,二次函数y=ax2+bx+2的图象与x轴交于点A(-1,0)、B(4,0),与y轴正半轴交于点C.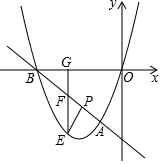 如图,直线y=-x-4与抛物线y=ax2+bx+c相交于A,B两点,其中A,B两点的横坐标分别为-1和-4,且抛物线过原点.
如图,直线y=-x-4与抛物线y=ax2+bx+c相交于A,B两点,其中A,B两点的横坐标分别为-1和-4,且抛物线过原点.