题目内容
16.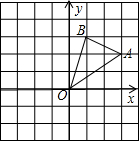 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,2),B(1,3)
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,2),B(1,3)(1)OA=$\sqrt{13}$,OB=$\sqrt{10}$AB=$\sqrt{5}$;
(2)试问:∠ABO是直角吗?请说明理由;
(3)将点A在网格上做上下移动,当点A在什么位置时,△AOB直角三角形?
分析 (1)根据勾股定理得到OA,OB,AB;
(2)根据勾股定理的逆定理即可判定∠ABO是否直角;
(3)根据平移的性质和直角三角形的判定和性质即可求解.
解答 解:(1)OA=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,OB=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,AB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$;
(2)∵($\sqrt{10}$)2+($\sqrt{5}$)2≠($\sqrt{13}$)2,
∴∠ABO不是直角;
(3)将点A在网格上做上下移动,当点A在(3,-1)位置时,△AOB直角三角形.
故答案为:$\sqrt{13}$,$\sqrt{10}$,$\sqrt{5}$.
点评 本题考查了勾股定理,勾股定理的逆定理,解答本题的关键根据勾股定理得到OA,OB,AB.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
6.二次函数y1=a(x-x1)(x-x2)(a≠0,x1≠x2)的图象与一次函数y2=bx+c(b≠0)的图象交于点(x1,0),若函数y=y1-2y2的图象经过点(x2,1),则有( )
| A. | 2b(x1-x2)=1 | B. | 2b(x2-x1)=1 | C. | b(x1-x2)=2 | D. | b(x2-x1)=2 |
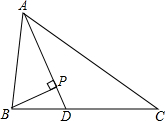 如图,△ABC中,AD平分∠BAC,BP⊥AD于点P,AB=5,BP=1,AC=9,说明∠ABP=2∠ACB的理由.
如图,△ABC中,AD平分∠BAC,BP⊥AD于点P,AB=5,BP=1,AC=9,说明∠ABP=2∠ACB的理由.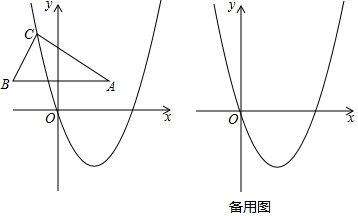
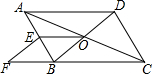 如图,在?ABCD中,对角线AC,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD.
如图,在?ABCD中,对角线AC,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD.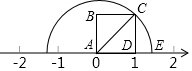 如图,四边形ABCD是正方形,点E表示的数是$\sqrt{2}$.
如图,四边形ABCD是正方形,点E表示的数是$\sqrt{2}$. 如图,二次函数y=ax2+bx+2的图象与x轴交于点A(-1,0)、B(4,0),与y轴正半轴交于点C.
如图,二次函数y=ax2+bx+2的图象与x轴交于点A(-1,0)、B(4,0),与y轴正半轴交于点C.