题目内容
16.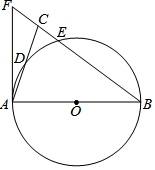 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于D、E两点,BC的延长线与⊙O的切线AF交于点F,连接BD.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于D、E两点,BC的延长线与⊙O的切线AF交于点F,连接BD.(1)求证:∠CAF=∠CBD;
(2)若AC=2$\sqrt{10}$,CE:EB=1:4,求AF的长.
分析 (1)连接BD,由AB为直径可得出BD⊥AC,结合等腰三角形的性质即可得出∠CBD=∠ABD,再由切线的性质即可得出∠FAB=∠CAF+∠CAB=90°,由同角的余角相等即可证出∠CAF=∠CBD;
(2)连接AE,设CE=a,则EB=4a,BA=BC=5a,由AB为直径可得出∠AEB=90°,利用勾股定理即可得出AE=3a,结合∠B=∠B即可证出△AEB∽△FAB,根据相似三角形的性质即可得出AF=$\frac{12}{5}$a,在Rt△AEC中,利用勾股定理即可求出a值,将其代入AF=$\frac{12}{5}$a中即可得出结论.
解答 (1)证明:连接BD,如图1所示.
∵AB为直径,
∴∠ADB=90°,
∴BD⊥AC.
∵BA=BC,
∴AD=CD,∠CBD=∠ABD.
∵AF与⊙O相切,
∴∠FAB=∠CAF+∠CAB=90°.
又∵∠CAB+∠ABD=90°,
∴∠CAF=∠ABD=∠CBD.
(2)解:连接AE,如图2所示.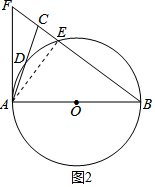
设CE=a,则EB=4a,BA=BC=5a.
∵AB为直径,
∴∠AEB=90°,
∴AE=$\sqrt{A{B}^{2}-E{B}^{2}}$=3a.
∵∠B=∠B,∠AEB=∠FAB=90°,
∴△AEB∽△FAB,
∴$\frac{FA}{AE}=\frac{EB}{AB}$,
∴FA=$\frac{AE•EB}{AB}$=$\frac{12}{5}$a.
在Rt△AEC中,AE=3a,CE=a,AC=2$\sqrt{10}$,
∴AE2+CE2=AC2,即9a2+a2=40,
解得:a=2或a=-2(舍去),
∴AF=$\frac{12}{5}$a=$\frac{24}{5}$.
点评 本题考查了相似三角形的判定与性质、等腰三角形的性质、切线的性质以及勾股定理,解题的关键是:(1)根据同角的余角相等找出∠CAF=∠ABD;(2)根据相似三角形的性质找出AF=$\frac{12}{5}$CE.

 名校课堂系列答案
名校课堂系列答案| A. | (1,4) | B. | (-1,-4) | C. | (4,-1) | D. | (1,-4) |
| A. | 0 | B. | -1 | C. | -50 | D. | 51 |
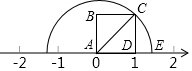 如图,四边形ABCD是正方形,点E表示的数是$\sqrt{2}$.
如图,四边形ABCD是正方形,点E表示的数是$\sqrt{2}$. 如图所示,数轴上点A所表示的数为-1+$\sqrt{5}$.
如图所示,数轴上点A所表示的数为-1+$\sqrt{5}$.