题目内容
2.已知,如图1,D是△ABC的边上一点,CN∥AB,DN交AC于点M,MA=MC.(1)求证:四边形ADCN是平行四边形.
(2)如图2,若∠AMD=2∠MCD,∠ACB=90°,AC=BC.请写出图中所有与线段AN相等的线段(线段AN除外)
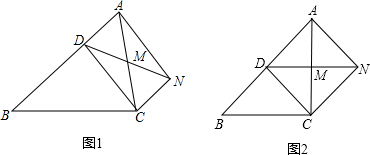
分析 (1)由CN∥AB,MA=MC,易证得△AMD≌△CMN,则可得MD=MN,即可证得:四边形ADCN是平行四边形.
(2)由∠AMD=2∠MCD,可证得四边形ADCN是矩形,又由∠ACB=90°,AC=BC,可得四边形ADCN是正方形,继而求得答案.
解答 (1)证明:∵CN∥AB,
∴∠DAM=∠NCM,
在△ADM和△CNM中,
$\left\{\begin{array}{l}{∠DAM=∠NCM}\\{MA=MC}\\{∠AMD=∠CMN}\end{array}\right.$,
∴△AMD≌△CMN(ASA),
∴MD=MN,
∴四边形ADCN是平行四边形.
(2)解:∵∠AMD=2∠MCD,∠AMD=∠MCD+∠MDC,
∴∠MCD=∠MDC,
∴MC=MD,
∴AC=DN,
∴?ADCN是矩形,
∵AC=BC,
∴AD=BD,
∵∠ACB=90°,
∴CD=AD=BD=$\frac{1}{2}$AB,
∴?ADCN是正方形,
∴AN=AD=BD=CD=CN.
点评 此题考查了平行四边形的判定与性质、正方形的判定与性质以及全等三角形的判定与性质等知识.注意证得△AMD≌△CMN与四边形ADCN是正方形是解此题的关键.

练习册系列答案
相关题目
12. 如图,直线AB∥CD,直线EF与直线AB相交于点M,MN平分∠AME,若∠1=50°,则∠2的度数为( )
如图,直线AB∥CD,直线EF与直线AB相交于点M,MN平分∠AME,若∠1=50°,则∠2的度数为( )
 如图,直线AB∥CD,直线EF与直线AB相交于点M,MN平分∠AME,若∠1=50°,则∠2的度数为( )
如图,直线AB∥CD,直线EF与直线AB相交于点M,MN平分∠AME,若∠1=50°,则∠2的度数为( )| A. | 50° | B. | 80° | C. | 85° | D. | 100° |
17.下列计算正确的是( )
| A. | 3$\sqrt{2}$-2$\sqrt{3}$=1 | B. | $\root{3}{-27}$=-3 | C. | |$\sqrt{2}$-$\sqrt{3}$|+$\sqrt{2}$=2$\sqrt{2}$-$\sqrt{3}$ | D. | ($\sqrt{3}$+$\frac{1}{\sqrt{3}}$)÷$\sqrt{3}$=4 |
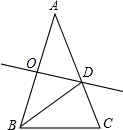 如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,以下结论:
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,以下结论:
 完成下面证明:如图,B是射线AD上一点,∠DAE=∠CAE,∠DAC=∠C=∠CBE
完成下面证明:如图,B是射线AD上一点,∠DAE=∠CAE,∠DAC=∠C=∠CBE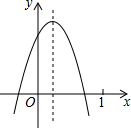 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程ax2+bx+c=0的两根之和大于0;④a-b+c<0,其中正确的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程ax2+bx+c=0的两根之和大于0;④a-b+c<0,其中正确的个数是( ) 如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,过D作DE∥BC交AB于点E,DF∥AB交BC于点F,连接EF.
如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,过D作DE∥BC交AB于点E,DF∥AB交BC于点F,连接EF.