题目内容
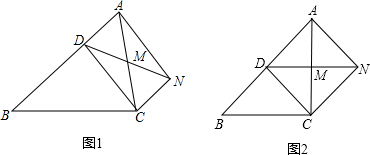
14. 完成下面证明:如图,B是射线AD上一点,∠DAE=∠CAE,∠DAC=∠C=∠CBE
完成下面证明:如图,B是射线AD上一点,∠DAE=∠CAE,∠DAC=∠C=∠CBE(1)求证:∠DBE=∠CBE
证明:∵∠C=∠CBE(已知)
∴BE∥AC内错角相等,两直线平行
∴∠DBE=∠DAC两直线平行,同位角相等
∵∠DAC=∠C(已知)
∴∠DBE=∠CBE等量代换
(2)请模仿(1)的证明过程,尝试说明∠E=∠BAE.
分析 (1)先根据平行线的判定定理得出BE∥AC,故可得出∠DBE=∠DAC,再由∠DAC=∠C即可得出结论;
(2)根据∠C=∠CBE得出BE∥AC,故∠CAE=∠E,再由∠DAE=∠CAE即可得出结论.
解答 (1)证明:∵∠C=∠CBE(已知),
∴BE∥AC(内错角相等,两直线平行),
∴∠DBE=∠DAC(两直线平行,同位角相等).
∵∠DAC=∠C(已知),
∴∠DBE=∠CBE(等量代换).
故答案为:内错角相等,两直线平行;两直线平行,同位角相等;等量代换;
(2)证明:∵∠C=∠CBE(已知),
∴BE∥AC(内错角相等,两直线平行 ),
∴∠CAE=∠E(两直线平行,内错角相等 ).
∵∠DAE=∠CAE(已知),
∴∠DAE=∠E(等量代换 ).
点评 本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
5.下列式子中不是整式的是( )
| A. | 9x | B. | $\frac{2b}{a}$ | C. | 0 | D. | $\frac{4b}{3}$-5a |
 如图,平行四边形ABCD的周长为12,对角线AC,BD相交于点O,点E是CD的中点,BD=4,则△DOE的周长为5.
如图,平行四边形ABCD的周长为12,对角线AC,BD相交于点O,点E是CD的中点,BD=4,则△DOE的周长为5.
 已知:如图,菱形ABCD的对角线AC,BD相交于O,点E,F分别是AD,DC的中点.已知OE=$\frac{5}{2}$,EF=3,求菱形ABCD的周长和面积.
已知:如图,菱形ABCD的对角线AC,BD相交于O,点E,F分别是AD,DC的中点.已知OE=$\frac{5}{2}$,EF=3,求菱形ABCD的周长和面积.