题目内容
7.如图1,正方形ABCD中,O是正方形对角线的交点,点E和点F是AD边和CD边上的两点(1)如果OE⊥OF,求证:OE=OF;
(2)如图2,点M为EF的中点,AE=DF,求证:DM=OM.

分析 (1)过O作OM⊥AD于M,ON⊥CD于N,求出∠MON=90°,求出OM=ON,∠EOM=∠FON,根据ASA推出△EOM≌△FON,根据全等三角形的性质得出即可;
(2)过O作ON⊥CD于N,OP⊥AD于P,求出∠PON=90°,求出OP=ON,PE=FN,根据SAS推出△EOP≌△FON,根据全等得出∠EOP=∠FON,求出∠EOF=90°,根据直角三角形斜边上的中线性质得出即可.
解答 证明:(1)如图1,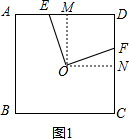
过O作OM⊥AD于M,ON⊥CD于N,则∠OMD=∠OND=90°,∠OME=∠ONF=90°,
∵四边形ABCD是正方形,
∴∠D=90°,
∴∠MON=360°-90°×3=90°,
∵O为正方形ABCD的对角线的交点,
∴OM=ON,
∵∠MON=90°,∠EOF=90°,
∴∠EOM=∠FON=90°-∠MOF,
在△EOM和△FON中
$\left\{\begin{array}{l}{∠EOM=∠FON}\\{OM=ON}\\{∠EMO=∠FNO}\end{array}\right.$
∴△EOM≌△FON(ASA),
∴OE=OF;
(2)如图2,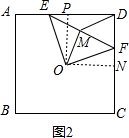
过O作ON⊥CD于N,OP⊥AD于P,
则∠OPD=∠OND=∠D=90°,
所以∠PON=90°,
∵O为正方形ABCD的对角线交点,
∴OP=ON,P、N分别为AD、CD的中点,
∵AE=DF,
∴PE=FN,
在△EOP和△FON中
$\left\{\begin{array}{l}{EP=FN}\\{∠EPO=∠FNO}\\{OP=ON}\end{array}\right.$
∴△EOP≌△FON(SAS),
∴∠EOP=∠FON,
∵∠PON=90°,
∴∠EOF=∠EOP+∠POF=∠FON+∠POF=∠PON=90°,
∵∠ADC=90°,M为EF的中点,
∴DM=$\frac{1}{2}$EF,OM=$\frac{1}{2}$EF,
∴DM=OM.
点评 本题考查了全等三角形的性质和判定,正方形的性质,直角三角形斜边上的中线性质的应用,能构造全等三角形是解此题的关键.

| A. | a2-2ab+b2 | B. | 4m2-2m+$\frac{1}{4}$ | C. | 9-6y+y2 | D. | x2-2xy-y2 |
| A. | 2x与-3x | B. | -m2n与8nm2 | C. | 4m2n与-7mn2 | D. | 10和-1 |
| A. | 若两个实数相等,则这两个实数的平方相等 | |
| B. | 若两个角是直角,则这两个角相等 | |
| C. | 若AB=5,BC=4,CA=3,则△ABC是直角三角形 | |
| D. | 若一个四边形的对角线互相垂直且平分,则这个四边形是菱形 |
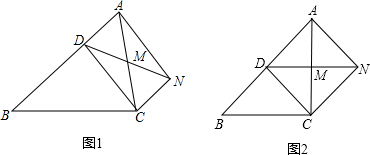
 如图,∠BAP+∠APD=180°,∠AOE=∠1,∠FOP=∠2.
如图,∠BAP+∠APD=180°,∠AOE=∠1,∠FOP=∠2.
 如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限内,对角线BD与x轴平行,直线y=x+3与x轴、y轴分别交于点E,F.将菱形ABCD沿x轴向左平移m(m>0)个单位,当点D落在△EOF的内部时(不包括三角形的边),则m的取值范围是4<m<6.
如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限内,对角线BD与x轴平行,直线y=x+3与x轴、y轴分别交于点E,F.将菱形ABCD沿x轴向左平移m(m>0)个单位,当点D落在△EOF的内部时(不包括三角形的边),则m的取值范围是4<m<6.