Question

13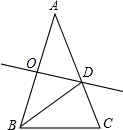．如图，在△ABC中，∠A=36°，AB=AC，AB的垂直平分线OD交AB于点O，交AC于点D，连接BD，以下结论：
①∠C=2∠A；
②BD平分∠ABC；
③S_△BCD=S_△BDO；
④点D到线段BC的距离等于线段OD的长．
其中正确的是①②④（把所有正确结论的序号都填在横线上）

Answer 1

分析 ①根据等腰三角形的性质再通过角的计算可得出∠C=72°=2∠A；②根据垂直平分线的性质可得出DA=DB，再根据角的计算即可得出∠ABD=∠DBC，从而得出BD平分∠ABC；③过点D作DE⊥BC于点E，根据角平分线的性质可得出DO=DE，再结合公共边BD=BD，即可证出Rt△BOD≌Rt△BED（HL），由此即可得出S_△BDO=S_△BDE≠S_△BCD；④由③中的DO=DE，即可得出点D到线段BC的距离等于线段OD的长．综上即可得出结论．

解答 解：①∵在△ABC中，∠A=36°，AB=AC，
∴∠C=∠ABC=$\frac{1}{2}$（180°-∠A）=72°=2∠A，
∴①成立；
②∵DO为AB的垂直平分线，
∴DA=DB，
∴∠A=∠ABD，
∵∠ABC=2∠A，
∴∠ABD=∠DBC，
∴BD平分∠ABC，即②成立；
③过点D作DE⊥BC于点E，如图所示．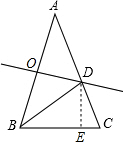
∵DO为AB的垂直平分线，
∴DO=DE，
在Rt△BOD和Rt△BED中，$\left\{\begin{array}{l}{BD=BD}\\{DO=DE}\end{array}\right.$，
∴Rt△BOD≌Rt△BED（HL），
∴S_△BDO=S_△BDE≠S_△BCD，
∴③不成立；
④∵DO=DE，
∴点D到线段BC的距离等于线段OD的长，
∴④正确．
综上可知：正确的结论是①②④．
故答案为：①②④．

点评 本题考查了等腰三角形的性质、线段垂直平分线的性质以及全等三角形的判定与性质，解题的关键是逐条分析4条选项．本题属于中档题，难度不大，解决该题型题目时，熟记垂直平分线和角平分线的性质是关键．