题目内容
如图，在△ABC中，已知点D、E、F分别为BC、AD、BE的中点，且S△ABC=8cm2，则图中阴影部分△CEF的面积是多少？考点：三角形的面积
专题：
分析：由点E为AD的中点，可得△ABC与△BCE的面积之比，同理可得，△BCE和△EFC的面积之比，即可解答出．
解答：解：如图，
∵E为AD的中点，
∴S△ABC：S△BCE=2：1，
同理可得，S△BCE：S△EFC=2：1，
∵S△ABC=8cm2，
∴S△EFC=
S△ABC=
×8=2cm2．
∵E为AD的中点，
∴S△ABC：S△BCE=2：1，
同理可得，S△BCE：S△EFC=2：1，
∵S△ABC=8cm2，
∴S△EFC=
| 1 |
| 4 |
| 1 |
| 4 |
点评：本题主要考查了三角形面积及三角形面积的等积变换，三角形的中线将三角形分成面积相等的两部分．
练习册系列答案
相关题目
如图MN∥PQ∥BC，且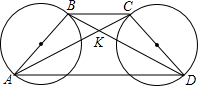
如图，梯形ABCD两对角线交于点K，分别以AB、CD为直径各作一圆，K位于两圆之外．证明：由点K向这两个圆所作的切线长相等．