题目内容
18.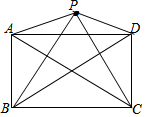 如图,已知P是矩形ABCD外一点,PA⊥PC,求证:PB⊥PD.
如图,已知P是矩形ABCD外一点,PA⊥PC,求证:PB⊥PD.
分析 证明A、B、C、D、P五点共圆,由圆周角定理∠BPD=∠BAD=90°,即可得出结论.
解答 证明:∵四边形ABCD是矩形,
∴∠ABC=∠ADC=∠BAD=90°,AB=DC,
∴∠ABC+∠ADC=180°,
∴A、B、C、D四点共圆,AC、BD是直径,
∵PA⊥PC,
∴∠APC=90°,
∴点P也在这个圆上,
即A、B、C、D、P五点共圆,
∴∠BPD=∠BAD=90°,
∴PB⊥PD.
点评 本题考查了矩形的性质、五点共圆、圆周角定理等知识;熟练掌握矩形的性质,证明五点共圆是解决问题的关键.

练习册系列答案
相关题目
10.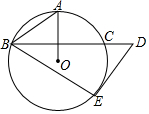 如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是( )
如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是( )
 如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是( )
如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是( )| A. | 52° | B. | 58° | C. | 60° | D. | 64° |
7.若关于x的一元二次方程$\frac{\sqrt{3}}{4}$x2+$\sqrt{3}$x+tana=0有两个相等的实数根,则锐角a等于( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
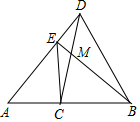 如图,已知点C为线段AB的中点,以BC为边作△DBC,使DC=DB,连接AD,过点C作CE⊥AB交AD于点E,连接BE交CD于点M.
如图,已知点C为线段AB的中点,以BC为边作△DBC,使DC=DB,连接AD,过点C作CE⊥AB交AD于点E,连接BE交CD于点M.