题目内容
10.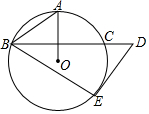 如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是( )
如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是( )| A. | 52° | B. | 58° | C. | 60° | D. | 64° |
分析 如图连接OE,设OA交BC于H.根据四边形内角和定理求出∠HOD,再根据∠ABE=$\frac{1}{2}$∠AOE即可解决问题.
解答 解:如图连接OE,设OA交BC于H.
∵DE是⊙O的切线,
∴OE⊥DE,
∴∠OED=90°,
∵BC⊥OA于H,
∴∠OHD=90°,
∴∠EOH=360°-∠OHD-∠D-∠OED=360°-90°-52°-90°=128°,
∴∠ABE=$\frac{1}{2}$∠AOE=64°,
故选D.
点评 本题考查切线的性质,四边形内角和定理,圆周角定理等知识,解题的关键是学会添加常用辅助线,学会用转化的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
5.国家体育馆“鸟巢”的建筑面积达25.8万平方米,请将“25.8万”用科学记数法表示,结果是( )
| A. | 25.8×104 | B. | 25.8×105 | C. | 2.58×104 | D. | 2.58×105 |
19.设x1,x2是方程x2-4x+m=0的两个根,且x1+x2-x1x2=1,那么m的值为( )
| A. | 2 | B. | -3 | C. | 3 | D. | -2 |
 如图,四边形ABCD中,BD与AC相交于E点,AE=CE,BC=AC=DC,则tan∠ABD•tan∠ADB=$\frac{1}{3}$.
如图,四边形ABCD中,BD与AC相交于E点,AE=CE,BC=AC=DC,则tan∠ABD•tan∠ADB=$\frac{1}{3}$.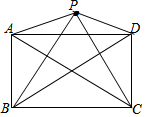 如图,已知P是矩形ABCD外一点,PA⊥PC,求证:PB⊥PD.
如图,已知P是矩形ABCD外一点,PA⊥PC,求证:PB⊥PD. 如图,点A的坐标为(1,2),AB⊥x轴于点B,将△AOB绕点A逆时针旋转90°得到△ACD,双曲线y=$\frac{k}{x}$(x>0)恰好经过点C,交AD于点E,则点E的坐标为($\frac{3}{2}$,2).
如图,点A的坐标为(1,2),AB⊥x轴于点B,将△AOB绕点A逆时针旋转90°得到△ACD,双曲线y=$\frac{k}{x}$(x>0)恰好经过点C,交AD于点E,则点E的坐标为($\frac{3}{2}$,2).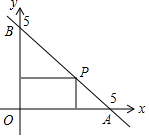 如图,一次函数的图象与两坐标轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长是( )
如图,一次函数的图象与两坐标轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长是( )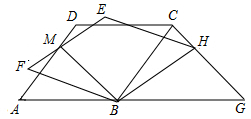 如图,菱形ABCD边长为5,tan∠DAB=$\frac{4}{3}$,将菱形绕点B按顺时针方向旋转角α(0°<α<∠DBA)得到菱形FBHE(点A的对应点为点F),EF与AD交于点M,连接BM.
如图,菱形ABCD边长为5,tan∠DAB=$\frac{4}{3}$,将菱形绕点B按顺时针方向旋转角α(0°<α<∠DBA)得到菱形FBHE(点A的对应点为点F),EF与AD交于点M,连接BM.