题目内容
7．若关于x的一元二次方程$\frac{\sqrt{3}}{4}$x2+$\sqrt{3}$x+tana=0有两个相等的实数根，则锐角a等于（ ）| A． | 15° | B． | 30° | C． | 45° | D． | 60° |
分析 由方程有两个相等的实数根得出△=3-4×$\frac{\sqrt{3}}{4}$tana=0，求得tana的值即可得出答案．
解答 解：∵方程$\frac{\sqrt{3}}{4}$x2+$\sqrt{3}$x+tana=0有两个相等的实数根，
∴△=3-4×$\frac{\sqrt{3}}{4}$tana=0，
解得：tana=$\sqrt{3}$，
则锐角a等于60°，
故选：D．
点评 本题主要考查根的判别式，熟练掌握根的判别式与方程的根之间的关系是解题的关键．
练习册系列答案
相关题目
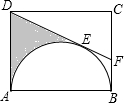矩形ABCD中，AB=6，以AB为直径在矩形内作半圆，与DE相切于点E（如图），延长DE交BC于F，若BF=$\sqrt{3}$，则阴影部分的面积为9$\sqrt{3}$-3π．
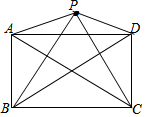如图，已知P是矩形ABCD外一点，PA⊥PC，求证：PB⊥PD．
如图，点A的坐标为（1，2），AB⊥x轴于点B，将△AOB绕点A逆时针旋转90°得到△ACD，双曲线y=$\frac{k}{x}$（x＞0）恰好经过点C，交AD于点E，则点E的坐标为（$\frac{3}{2}$，2）．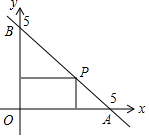
如图，一次函数的图象与两坐标轴分别交于A，B两点，P是线段AB上任意一点（不包括端点），过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长是（ ）
19．设x1，x2是方程x2-4x+m=0的两个根，且x1+x2-x1x2=1，那么m的值为（ ）
| A． | 2 | B． | -3 | C． | 3 | D． | -2 |
