题目内容
1.若关于x的分式方程$\frac{m}{2-x}$-1=1-$\frac{x}{x-2}$的解为正数,且关于y的不等式组$\left\{\begin{array}{l}{\frac{2y-5}{3}≤-3}\\{y-m-1>-1}\end{array}\right.$无解,那么符合条件的所有整数m的和为( )| A. | 5 | B. | 3 | C. | 1 | D. | 0 |
分析 根据题意可以求得m的取值范围,从而可以得到符合条件的m的整数值,从而可以解答本题.
解答 解:由方程$\frac{m}{2-x}$-1=1-$\frac{x}{x-2}$,解得,x=4-m,
则$\left\{\begin{array}{l}{4-m>0}\\{4-m≠2}\end{array}\right.$,
解得,m<4且m≠2,
∵关于y的不等式组$\left\{\begin{array}{l}{\frac{2y-5}{3}≤-3}\\{y-m-1>-1}\end{array}\right.$无解,
解得,m≥-2,
由上可得,m的取值范围是:-2≤m<4,且m≠2,
∴符合条件的所有整数m的和为:-2+(-1)+0+1+3=1,
故选C.
点评 本题考查分式方程的解、解一元一次不等式(组)、一元一次不等式组的整数解,解答本题的关键是明确题意,找出所求问题需要的条件,利用不等式的性质解答.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
16.在平面直角坐标系中,P(x,y)在第四象限,且|x|=2,|y|=3,则点P'(x,-y)的坐标( )
| A. | (-2,3) | B. | (2,3) | C. | (3,-2) | D. | (3,2) |
13.某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件,则x应满足的方程为( )
| A. | $\frac{720}{48+x}$-$\frac{720}{x}$=5 | B. | $\frac{720}{48}$+5=$\frac{720}{48+x}$ | C. | $\frac{720}{48}$-$\frac{720}{x}$=5 | D. | $\frac{720}{48}$-$\frac{720}{48+x}$=5 |
15.2017年春节黄金周宜春市共接待游客2234000人次,将2234000用科学记数法表示为( )
| A. | 22.34×105 | B. | 2.234×105 | C. | 2.234×106 | D. | 0.2234×107 |
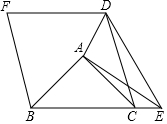 如图,△ABC与△AED都是等腰直角三角形,∠BAC=90°,AB=AC,∠DAE=90°,AD=AE,点B、C、E在一直线上,
如图,△ABC与△AED都是等腰直角三角形,∠BAC=90°,AB=AC,∠DAE=90°,AD=AE,点B、C、E在一直线上,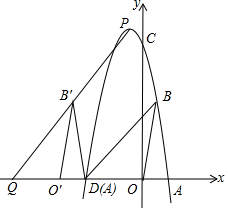 如图,已知A(2,0),B(1,m2-4m+5).
如图,已知A(2,0),B(1,m2-4m+5).