题目内容
若n为正整数，则（2n+1）2-1能否被8整除？请说明理由．
考点：因式分解-运用公式法
专题：
分析：直接利用完全平方公式展开，进而合并求出即可．
解答：解：（2n+1）2-1不能被8整除，
理由：（2n+1）2-1
=4n2+4n+1-1
=4n（n+1），
∵n为正整数，
∴n（n+1）为相邻整数，必有一个是2的倍数，
∴4n（n+1）能被8整除，
故（2n+1）2-1能被8整除．
理由：（2n+1）2-1
=4n2+4n+1-1
=4n（n+1），
∵n为正整数，
∴n（n+1）为相邻整数，必有一个是2的倍数，
∴4n（n+1）能被8整除，
故（2n+1）2-1能被8整除．
点评：此题主要考查了公式法的应用，熟练掌握完全平方公式是解题关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
如图，在△ABC中，AB=AC，BE=AE，△BCE的周长为12，BC=5，求AB的长．
如图所示，AB∥CD，∠A=∠F，∠D=∠E，DE与AB，AF分别交于点G，O，试说明∠EOF的度数是一个定值，并求出∠EOF的度数．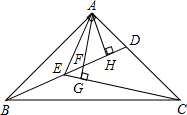
如图，△ABC中，AB=AC，∠BAC=90°，D为AC边上的一点，E在线段BD上，且∠AED=45°，连接CE，过A作AG⊥CE交BD于F，过A作AH⊥BD于H，探究FH与BE的数量关系，并证明．
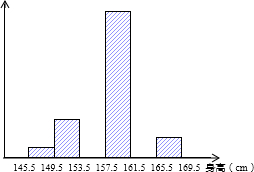为了解某学校八年级学生的身体发育情况，学校对八年级女生的身高进行了一次测量，所得数据整理后绘制出统计图（如图）．