题目内容
 如图所示,AB∥CD,∠A=∠F,∠D=∠E,DE与AB,AF分别交于点G,O,试说明∠EOF的度数是一个定值,并求出∠EOF的度数.
如图所示,AB∥CD,∠A=∠F,∠D=∠E,DE与AB,AF分别交于点G,O,试说明∠EOF的度数是一个定值,并求出∠EOF的度数.考点:平行线的性质,三角形内角和定理
专题:
分析:根据平行线的性质求出∠A=∠FMC,求出∠DCE=2∠F,根据三角形内角和定理求出∠E+∠F=90°,即可求出答案.
解答:解:
∵AB∥CD,
∴∠A=∠FMC,
∵∠A=∠F,∠DCE=∠F+∠FMC,
∴∠DCE=2∠F,
∵∠E=∠D,∠D+∠E+∠DCE=180°,
∴2∠E+2∠F=180°,
∴∠E+∠F=90°,
∴∠EOF=90°,
即∠EOF是一个定值,是90°.

∵AB∥CD,
∴∠A=∠FMC,
∵∠A=∠F,∠DCE=∠F+∠FMC,
∴∠DCE=2∠F,
∵∠E=∠D,∠D+∠E+∠DCE=180°,
∴2∠E+2∠F=180°,
∴∠E+∠F=90°,
∴∠EOF=90°,
即∠EOF是一个定值,是90°.
点评:本题考查了平行线的性质,三角形内角和定理,三角形外角性质的应用,主要考查学生的推理和计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
x是两位数,y是一位数,如果把x置于y的左边,那么所成的三位数应表示为( )
| A、xy | B、x+y |
| C、100x+y | D、10x+y |
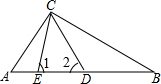 如图,在△ABC中,AD=AC,BE=BC.
如图,在△ABC中,AD=AC,BE=BC.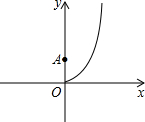 二次函数y=ax2(a≠0)的图象的一部分如图所示,点A的坐标为(0,1).以OA为边向右作等腰直角△OPA.若点P落在抛物线y=ax2上,求a的值.
二次函数y=ax2(a≠0)的图象的一部分如图所示,点A的坐标为(0,1).以OA为边向右作等腰直角△OPA.若点P落在抛物线y=ax2上,求a的值.