题目内容
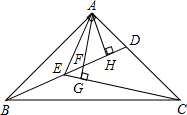 如图,△ABC中,AB=AC,∠BAC=90°,D为AC边上的一点,E在线段BD上,且∠AED=45°,连接CE,过A作AG⊥CE交BD于F,过A作AH⊥BD于H,探究FH与BE的数量关系,并证明.
如图,△ABC中,AB=AC,∠BAC=90°,D为AC边上的一点,E在线段BD上,且∠AED=45°,连接CE,过A作AG⊥CE交BD于F,过A作AH⊥BD于H,探究FH与BE的数量关系,并证明.考点:全等三角形的判定与性质
专题:
分析:延长AH交CE于P,根据ASA证得△ABF≌△APC,证得BF=AP,根据AAS证得△AHF≌△EHP,得出FH=PH,根据△AEH是等腰直角三角形,则AH=EH,则BE+EH-FH=AH+HP,从而求得BE=2FH.
解答: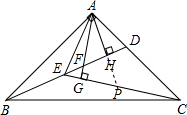 答:FH与BE的数量关系为:BE=2FH,
答:FH与BE的数量关系为:BE=2FH,
证明:延长AH交CE于P,
∵∠ABF+∠ADB=90°,∠PAC+∠ADB=90°,
∴∠ABF=∠PAC,
∵AG⊥CE,AH⊥BD,∠EFG=∠AFH,
∴∠FEG=∠FAH,
∵∠FAH+∠AFH=90°,∠FEG+∠EPH=90°,
∴∠AFH=∠EPH,
∴∠AFB=∠APC,
在△ABF与△APC中,
,
∴△ABF≌△APC(ASA),
∴BF=AP,
∵AH⊥BD,∠AED=45°,
∴AH=EH,
在△AHF与△EHP中,
,
∴△AHF≌△EHP(AAS),
∴FH=PH,
∴BE+EH-FH=AH+HP,
∴BE=2FH.
 答:FH与BE的数量关系为:BE=2FH,
答:FH与BE的数量关系为:BE=2FH,证明:延长AH交CE于P,
∵∠ABF+∠ADB=90°,∠PAC+∠ADB=90°,
∴∠ABF=∠PAC,
∵AG⊥CE,AH⊥BD,∠EFG=∠AFH,
∴∠FEG=∠FAH,
∵∠FAH+∠AFH=90°,∠FEG+∠EPH=90°,
∴∠AFH=∠EPH,
∴∠AFB=∠APC,
在△ABF与△APC中,
|
∴△ABF≌△APC(ASA),
∴BF=AP,
∵AH⊥BD,∠AED=45°,
∴AH=EH,
在△AHF与△EHP中,
|
∴△AHF≌△EHP(AAS),
∴FH=PH,
∴BE+EH-FH=AH+HP,
∴BE=2FH.
点评:本题考查了等腰直角三角形的性质以及全等三角形的判定和性质,延长AH交CE于P,构建两组全等的三角形是本题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目

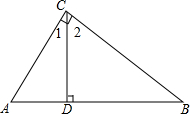 如图,Rt△ABC中,∠ACB=90°,CD是AB边上的高,写出分别与∠1,∠2相等的角,并说明理由.
如图,Rt△ABC中,∠ACB=90°,CD是AB边上的高,写出分别与∠1,∠2相等的角,并说明理由.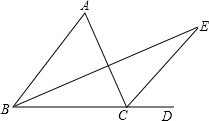 如图,在△ABC中,D是BC延长线上的一点,∠ABC,∠ACD的角平分线交于点E.求证:∠E=
如图,在△ABC中,D是BC延长线上的一点,∠ABC,∠ACD的角平分线交于点E.求证:∠E=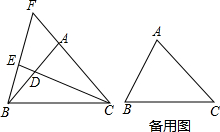 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD于E,交直线AC于F.
如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD于E,交直线AC于F.