题目内容
 如图所示,在四边形机器零件ABCD中,∠B=∠D=90°,∠A=60°,AB=10,CD=6,求这个四边形的面积(提示:在直角三角形中,30°的角所对的直角边等于斜边的一半).
如图所示,在四边形机器零件ABCD中,∠B=∠D=90°,∠A=60°,AB=10,CD=6,求这个四边形的面积(提示:在直角三角形中,30°的角所对的直角边等于斜边的一半).考点:勾股定理的应用,含30度角的直角三角形
专题:
分析:延长AD、BC交于E,根据直角三角形两锐角互余求出∠E=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半求出AE、CE,再利用勾股定理列式求出BE、DE,然后根据四边形的面积等于两个直角三角形的面积的差列式计算即可得解.
解答: 如图,延长AD、BC交于E.
如图,延长AD、BC交于E.
∵∠B=90°,∠A=60°,
∴∠E=90°-60°=30°,
在Rt△ABE和Rt△CDE中,∵AB=10,CD=6,
∴AE=2AB=20,CE=2CD=2×6=12,
由勾股定理得,BE=
=10
,
DE=
=6
,
∴S四边形ABCD=
×10
×10-
×6
×6
=50
-18
=32
.
 如图,延长AD、BC交于E.
如图,延长AD、BC交于E.∵∠B=90°,∠A=60°,
∴∠E=90°-60°=30°,
在Rt△ABE和Rt△CDE中,∵AB=10,CD=6,
∴AE=2AB=20,CE=2CD=2×6=12,
由勾股定理得,BE=
| 202-102 |
| 3 |
DE=
| 122-62 |
| 3 |
∴S四边形ABCD=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
=50
| 3 |
| 3 |
=32
| 3 |
点评:本题考查了二次根式的化简,勾股定理,直角三角形30°角所对的直角边等于斜边的一半的性质,三角形的面积,作辅助线构造出直角三角形是解题的关键.

练习册系列答案
相关题目
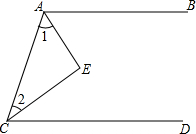 如图,AE、CE分别平分∠BAC和∠ACD,∠1和∠2互余,试说明AB∥CD.
如图,AE、CE分别平分∠BAC和∠ACD,∠1和∠2互余,试说明AB∥CD. 如图,△ABC中,∠A=40°∠B=76°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,求∠CDF的度数.
如图,△ABC中,∠A=40°∠B=76°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,求∠CDF的度数.