题目内容
弦AB把圆周分成1:3的两部分,点C是圆上不同于A、B的一点,那么∠ACB的度数为 .
考点:圆周角定理
专题:分类讨论
分析:首先根据题意画出图形,然后由圆的一条弦把圆周分成1:3两部分,求得∠AOB的度数,又由圆周角定理,求得∠ACB的度数,然后根据圆的内接四边形的对角互补,求得∠AC′B的度数,继而可求得答案.
解答: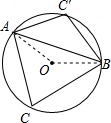 解:∵弦AB把⊙O分成1:3两部分,
解:∵弦AB把⊙O分成1:3两部分,
∴∠AOB=
×360°=90°,
∴∠ACB=
∠AOB=45°,
∵四边形AC′BC是⊙O的内接四边形,
∴∠AC′B=180°-∠ACB=135°.
∴这条弦所对的圆周角的度数是:45°或135°.
故答案为:45°或135°.
 解:∵弦AB把⊙O分成1:3两部分,
解:∵弦AB把⊙O分成1:3两部分,∴∠AOB=
| 1 |
| 4 |
∴∠ACB=
| 1 |
| 2 |
∵四边形AC′BC是⊙O的内接四边形,
∴∠AC′B=180°-∠ACB=135°.
∴这条弦所对的圆周角的度数是:45°或135°.
故答案为:45°或135°.
点评:此题考查了圆周角定理与圆的内接四边形的性质,以及圆心角与弧的关系.此题难度不大,解题的关键是注意数形结合思想的应用.

练习册系列答案
相关题目
 如图,一个带数字的正方体的展开图,相对的两个面上的数字和最小的是( )
如图,一个带数字的正方体的展开图,相对的两个面上的数字和最小的是( )| A、3 | B、4 | C、5 | D、6 |
下列计算错误的是( )
| A、a3•a-2=a | ||
| B、a4÷a3=a2 | ||
| C、a3-3a3=-2a3 | ||
D、(-1+
|
下列说法正确的是( )
| A、三角形的一个外角大于一个内角 |
| B、三角形的一个外角等于两个内角之和 |
| C、相等的角是对顶角 |
| D、在同一平面内,垂直于同一直线的两条直线平行 |
 如图所示,在四边形机器零件ABCD中,∠B=∠D=90°,∠A=60°,AB=10,CD=6,求这个四边形的面积(提示:在直角三角形中,30°的角所对的直角边等于斜边的一半).
如图所示,在四边形机器零件ABCD中,∠B=∠D=90°,∠A=60°,AB=10,CD=6,求这个四边形的面积(提示:在直角三角形中,30°的角所对的直角边等于斜边的一半). 如图,E、F分别是平行四边形ABCD的边AD、BC的中点,若四边形AEFB与四边形ABCD相似,AB=4,则AD的长度为
如图,E、F分别是平行四边形ABCD的边AD、BC的中点,若四边形AEFB与四边形ABCD相似,AB=4,则AD的长度为 如图,∠ABC与∠ACB的平分线相交于F,过F作DE∥BC交AB于D,交AC于E.
如图,∠ABC与∠ACB的平分线相交于F,过F作DE∥BC交AB于D,交AC于E.