题目内容
已知抛物线y=ax2+bx经过点A(2,0)顶点为D(1,-1).
(1)确定抛物线的解析式;
(2)直线y=3与抛物线相交于B、C两点(B点在C点左侧),以B、点C及原点O为顶点作平行四边形.设平行四边形的另一顶点为Q,请求出点Q的坐标.
(3)若以(2)小题中BC为一边,抛物线的任一点P为另一顶点作为平行四边形,当平行四边形面积为8时,确定P点的坐标.
(1)确定抛物线的解析式;
(2)直线y=3与抛物线相交于B、C两点(B点在C点左侧),以B、点C及原点O为顶点作平行四边形.设平行四边形的另一顶点为Q,请求出点Q的坐标.
(3)若以(2)小题中BC为一边,抛物线的任一点P为另一顶点作为平行四边形,当平行四边形面积为8时,确定P点的坐标.
考点:二次函数综合题,解一元二次方程-配方法,平行四边形的性质,平移的性质
专题:综合题,分类讨论
分析:(1)可根据抛物线的顶点坐标将抛物线的解析式设成顶点式,然后把点A的坐标代入抛物线的顶点式,就可解决问题;
(2)可先求出点B、C的坐标,然后根据平行四边形的性质及平移的性质就可求出点Q的坐标;
(3)根据条件可求出点P到BC的距离,从而得到点P的纵坐标,然后将其代入抛物线的解析式,就可得到点P的坐标.
(2)可先求出点B、C的坐标,然后根据平行四边形的性质及平移的性质就可求出点Q的坐标;
(3)根据条件可求出点P到BC的距离,从而得到点P的纵坐标,然后将其代入抛物线的解析式,就可得到点P的坐标.
解答:解:(1)∵抛物线y=ax2+bx顶点为D(1,-1),
∴抛物线的解析式可设为y=a(x-1)2-1,
又∵该抛物线经过点A(2,0),
∴a(2-1)2-1=0,
∴a=1,
∴y=(x-1)2-1=x2-2x,
即抛物线的解析式为y=x2-2x;
(2)如图1,
当y=3时,x2-2x=3,
解得:x1=3,x2=-1,
∴B(-1,3),C(3,3),
∴BC=4.
①若BC为平行四边形的一边,
则OQ∥BC,且OQ=BC,
∴点Q在x轴上,且OQ=4,
∴点Q的坐标为(-4,0)或(4,0);
②若BC为平行四边形的一条对角线,
则OB∥CQ,且OB=CQ,
∴线段CQ可由线段OB平移所得.
∵点O(0,0)向右移动3个单位,再向上移动3个单位到达点C(3,3),
∴点B(-1,3)向右移动3个单位,再向上移动3个单位到达点Q,
∴点Q的坐标为(-1+3,3+3)即(2,6).
综上所述:符合条件的点Q的坐标为(-4,0)或(4,0)或(2,6);
 (3)过点P作PH⊥BC于点H,如图2,
(3)过点P作PH⊥BC于点H,如图2,
由题可得:S△PBC=
BC•PH=
×8=4,
∵BC=4,∴PH=2.
①当点P在BC下方时,yP=3-2=1,
由x2-2x=1得x3=1+
,x4=1-
,
∴点P的坐标为(1+
,1)或(1-
,1);
②当点P在BC上方时,yP=3+2=5,
由x2-2x=5得x5=1+
,x6=1-
,
∴点P的坐标为(1+
,5)或(1-
,5).
综上所述:满足条件的点P的坐标为(1+
,1)或(1-
,1)或(1+
,5)或(1-
,5).
∴抛物线的解析式可设为y=a(x-1)2-1,
又∵该抛物线经过点A(2,0),
∴a(2-1)2-1=0,
∴a=1,
∴y=(x-1)2-1=x2-2x,
即抛物线的解析式为y=x2-2x;
(2)如图1,
当y=3时,x2-2x=3,

解得:x1=3,x2=-1,
∴B(-1,3),C(3,3),
∴BC=4.
①若BC为平行四边形的一边,
则OQ∥BC,且OQ=BC,
∴点Q在x轴上,且OQ=4,
∴点Q的坐标为(-4,0)或(4,0);
②若BC为平行四边形的一条对角线,
则OB∥CQ,且OB=CQ,
∴线段CQ可由线段OB平移所得.
∵点O(0,0)向右移动3个单位,再向上移动3个单位到达点C(3,3),
∴点B(-1,3)向右移动3个单位,再向上移动3个单位到达点Q,
∴点Q的坐标为(-1+3,3+3)即(2,6).
综上所述:符合条件的点Q的坐标为(-4,0)或(4,0)或(2,6);
 (3)过点P作PH⊥BC于点H,如图2,
(3)过点P作PH⊥BC于点H,如图2,由题可得:S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∵BC=4,∴PH=2.
①当点P在BC下方时,yP=3-2=1,
由x2-2x=1得x3=1+
| 2 |
| 2 |
∴点P的坐标为(1+
| 2 |
| 2 |
②当点P在BC上方时,yP=3+2=5,
由x2-2x=5得x5=1+
| 6 |
| 6 |
∴点P的坐标为(1+
| 6 |
| 6 |
综上所述:满足条件的点P的坐标为(1+
| 2 |
| 2 |
| 6 |
| 6 |
点评:本题主要考查了运用待定系数法求抛物线的解析式、平行四边形的性质、平移的性质、解一元二次方程等知识,正确进行分类是解决本题的关键.

练习册系列答案
相关题目
若一个三角形的三边a,b,c满足a2-ab=ac-bc,则这个三角形的形状是( )
| A、直角三角形 | B、等边三角形 |
| C、等腰三角形 | D、无法判断 |

 如图所示,在四边形机器零件ABCD中,∠B=∠D=90°,∠A=60°,AB=10,CD=6,求这个四边形的面积(提示:在直角三角形中,30°的角所对的直角边等于斜边的一半).
如图所示,在四边形机器零件ABCD中,∠B=∠D=90°,∠A=60°,AB=10,CD=6,求这个四边形的面积(提示:在直角三角形中,30°的角所对的直角边等于斜边的一半). 如图所示,∠AOB=90°,OM是∠AOC的平分线,ON是∠BOC的平分线,∠MON=
如图所示,∠AOB=90°,OM是∠AOC的平分线,ON是∠BOC的平分线,∠MON=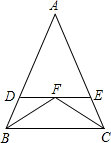 如图,∠ABC与∠ACB的平分线相交于F,过F作DE∥BC交AB于D,交AC于E.
如图,∠ABC与∠ACB的平分线相交于F,过F作DE∥BC交AB于D,交AC于E.