题目内容
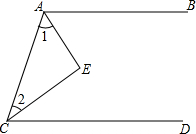如图，AE、CE分别平分∠BAC和∠ACD，∠1和∠2互余，试说明AB∥CD．考点：平行线的判定
专题：
分析：先根据角平分线的性质得出∠1=∠BAE，∠2=∠DCE，再根据∠1和∠2互余可知∠1+∠2=90°，故可得出∠1+∠BAE+∠2+∠DCE=180°，进而可得出结论．
解答：解：∵AE、CE分别平分∠BAC和∠ACD，
∴∠1=∠BAE，∠2=∠DCE．
∵∠1和∠2互余，
∴∠1+∠2=90°，
∴∠1+∠BAE+∠2+∠DCE=180°，
∴AB∥CD．
∴∠1=∠BAE，∠2=∠DCE．
∵∠1和∠2互余，
∴∠1+∠2=90°，
∴∠1+∠BAE+∠2+∠DCE=180°，
∴AB∥CD．
点评：本题考查的是平行线的判定，熟知同旁内角互补，两直线平行是解答此题的关键．
练习册系列答案
相关题目
如图所示，在四边形机器零件ABCD中，∠B=∠D=90°，∠A=60°，AB=10，CD=6，求这个四边形的面积（提示：在直角三角形中，30°的角所对的直角边等于斜边的一半）．
如图所示，△ABC中，若点O是∠B、∠C的角平分线的交点，且∠ABC=50°，∠ACB=60°，则∠OAB=