题目内容
 如图,在Rt△ABC中,∠C=90°,现将△ABC进行翻折,点C恰落在边AB上的点D处,折痕为EF,此时恰有∠DEF=∠A,则AD与BD的大小关系是
如图,在Rt△ABC中,∠C=90°,现将△ABC进行翻折,点C恰落在边AB上的点D处,折痕为EF,此时恰有∠DEF=∠A,则AD与BD的大小关系是考点:翻折变换(折叠问题)
专题:
分析:如图,作辅助线;首先证明D、E、C、F四点共圆,得到∠DEF=∠DCF;进而证明∠DCF=∠A,得到DA=DC;其次证明DB=DC,即可解决问题.
解答: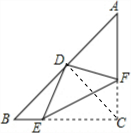 解:如图,连接CD;
解:如图,连接CD;
由题意得:∠EDF=∠ECF,
∴∠EDF+∠ECF=180°,
∴D、E、C、F四点共圆,
∴∠DEF=∠DCF;而∠DEF=∠A,
∴∠DCF=∠A(设为α),DA=DC;
∵∠B+α=∠BCD+α=90°,
∴∠B=∠BCD,
∴DB=DC,DA=DB,
故答案为AD=BD.
 解:如图,连接CD;
解:如图,连接CD;由题意得:∠EDF=∠ECF,
∴∠EDF+∠ECF=180°,
∴D、E、C、F四点共圆,
∴∠DEF=∠DCF;而∠DEF=∠A,
∴∠DCF=∠A(设为α),DA=DC;
∵∠B+α=∠BCD+α=90°,
∴∠B=∠BCD,
∴DB=DC,DA=DB,
故答案为AD=BD.
点评:该题主要考查了旋转变换的性质、四点共圆的判定、等腰三角形的判定等知识点的应用问题;解题的关键是作辅助线.

练习册系列答案
相关题目
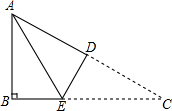 如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE的长为( )
如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示,a∥b,∠1=158°,∠2=42°,∠4=50°.那么∠3=( )
如图所示,a∥b,∠1=158°,∠2=42°,∠4=50°.那么∠3=( )| A、50° | B、60° |
| C、70° | D、80° |

 A,B分别为河两岸的两点,其距离不能直接测出,请你根据所学的知识写出一个测量A,B两点之间距离的方法,要求:画出图形,写出已知和求证,并证明.
A,B分别为河两岸的两点,其距离不能直接测出,请你根据所学的知识写出一个测量A,B两点之间距离的方法,要求:画出图形,写出已知和求证,并证明. 已知数轴上一点A对应的数为4.
已知数轴上一点A对应的数为4.