题目内容
已知在△ABC中，AD是△BAC的平分线，将△ADC沿AD翻折，点C的对称点为E，若AC=2，BE=1，则AB= ．
考点：翻折变换（折叠问题）
专题：
分析：如图，运用翻折变换的性质，结合已知条件得到点C的对称点E与点A、B共线，求出AE，即可解决问题．
解答：
解：如图，∵AD是△BAC的平分线，
∴将△ADC沿AD翻折，
点C的对称点E与点A、B共线；
由翻折变换的性质得：
AE=AC=2，而BE=1，
∴AB=2-1=1．
故答案为1．
解：如图，∵AD是△BAC的平分线，∴将△ADC沿AD翻折，
点C的对称点E与点A、B共线；
由翻折变换的性质得：
AE=AC=2，而BE=1，
∴AB=2-1=1．
故答案为1．
点评：该题主要考查了翻折变换的性质及其应用问题；判断、发现点A、B、E三点共线是解题的关键．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
如图，等边△ABC外一点P到三边距离分别为h1，h2，h3，且h3+h2-h1=3，其中PD=h3，PE=h2，PF=h1．则△ABC的面积S△ABC=
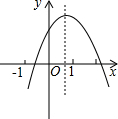已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①abc＞0 ②2a+b＜0 ③4a-2b+c＜0 ④
| 4ac-b2 |
| 4a |
其中正确结论的个数为（ ）
| A、4个 | B、3个 | C、2个 | D、1个 |
八年级（5）班开展了手工制作竞赛，每个同学都在规定时间内完成一件手工作品．小明同学在制作手工作品的第一、二个步骤是：①先裁下了一张长BC=20cm，宽AB=16cm的长方形纸片ABCD，②将纸片沿着直线AE折叠，点D恰好落在BC边上的点F处，…请你根据①②步骤解答下列问题：
如图，在Rt△ABC中，∠C=90°，现将△ABC进行翻折，点C恰落在边AB上的点D处，折痕为EF，此时恰有∠DEF=∠A，则AD与BD的大小关系是能同时把矩形的面积和周长分成相等两部分的直线有（ ）条．
| A、1条 | B、2条 | C、3条 | D、无数条 |
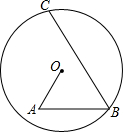如图，在圆O中，点A在圆内，B，C在圆上，其中OA=7，BC=18，∠A=∠B=60°，则OB=