Question

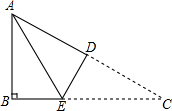如图所示，在△ABC中，∠B=90°，AB=3，AC=5，将△ABC折叠，使点C与点A重合，折痕为DE，则BE的长为（　　）

• A、

  25

  8

• B、

  7

  8

• C、

  25

  6

• D、

  7

  6

Answer 1

考点：翻折变换（折叠问题）

专题：

分析：如图，首先求出BC的长；根据勾股定理列出关于CE的方程，求出CE，即可解决问题．

解答：解：如图，∵∠B=90°，AB=3，AC=5，
∴BC=

52-32

=4；由题意得：
AE=CE（设为λ），则BE=4-λ；
由勾股定理得：λ²=（4-λ）²+3²，
解得：λ=

25

8

，
∴BE=4-λ=

7

8

．
故选D．

点评：该题主要考查了翻折变换的性质及其应用问题；解题的关键是准确找出图形中隐含的相等或全等关系．