题目内容
19.设x1,x2是一元二次方程x2+2x-1=0的两个限,则2x12+5x1+x2的值为( )| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
分析 先根据一元二次方程的解的定义得到x12+2x1-1=0,即x12=-2x1+1,则2x12+5x1+x2可化将为x1+x2+2,再根据根与系数的关系得到x1+x2=-2,然后利用整体代入的方法计算.
解答 解:∵x1是一元二次方程x2+2x-1=0的限,
∴x12+2x1-1=0,即x12=-2x1+1,
∴2x12+5x1+x2=2(-2x1+1)+5x1+x2=x1+x2+2,
∵x1,x2是一元二次方程x2+2x-1=0的两个限,
∴x1+x2=-2,
∴2x12+5x1+x2=-2+2=0.
故选C.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.也考查了一元二次方程的解.

练习册系列答案
相关题目
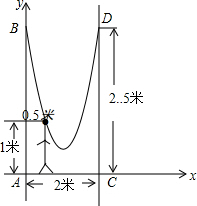 如图,小明的父亲在相距2米的两棵树(AB、CD)间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子.以A为原点,AC所在直线为x轴,AB所在直线为y轴,建立如图所示的直角坐标系.
如图,小明的父亲在相距2米的两棵树(AB、CD)间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子.以A为原点,AC所在直线为x轴,AB所在直线为y轴,建立如图所示的直角坐标系.